江西省赣州市南康区2019-2020学年八年级下学期数学线上月考试卷
试卷更新日期:2020-07-29 类型:月考试卷
一、单选题
-
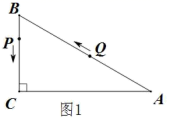
1. 如果 是二次根式,那么 应满足的条件是( )A、 B、 C、 D、2. 如图,在 中, , , ,则 的长为( )
 A、 B、 C、3 D、153. 下列计算或化简正确的是( )A、 B、 C、 D、4. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )
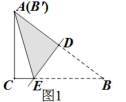
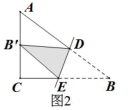
A、 B、 C、3 D、153. 下列计算或化简正确的是( )A、 B、 C、 D、4. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )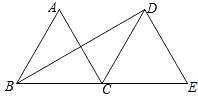 A、 B、 C、 D、5. 《九章算术》中的“折竹抵地”问题上:今有竹高一丈,末折抵地,去本六尺。问折高几何?意思是:如图,一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远。问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A、 B、 C、 D、5. 《九章算术》中的“折竹抵地”问题上:今有竹高一丈,末折抵地,去本六尺。问折高几何?意思是:如图,一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远。问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( ) A、 B、 C、x2+6=(10-x)2 D、x2+62=(10-x)26. 小华和小明计算 时,得出两种不同的答案,小华符合题意审题,得到的答案是“ ”,小明忽略了算式后面括号中的条件,得到的结果是“2”,请你判断,括号中的条件是( )A、 B、 C、 D、
A、 B、 C、x2+6=(10-x)2 D、x2+62=(10-x)26. 小华和小明计算 时,得出两种不同的答案,小华符合题意审题,得到的答案是“ ”,小明忽略了算式后面括号中的条件,得到的结果是“2”,请你判断,括号中的条件是( )A、 B、 C、 D、二、填空题
-
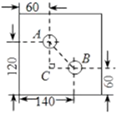
7. 计算: =.8. 在 中, , , ,则a的值是 .9. 一个三角形的三边长分别为 ,则它的周长是cm.10. 如图所示,是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位: )则两圆孔中心 和 的距离是 .
 11. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S= ,现已知△ABC的三边长分别为1,2, ,则△ABC的面积为 .
11. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S= ,现已知△ABC的三边长分别为1,2, ,则△ABC的面积为 . 12. 有一直角三角形两直角边分别为6 、8 ,在其外部拼上一个以8 为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是 .
12. 有一直角三角形两直角边分别为6 、8 ,在其外部拼上一个以8 为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是 .三、解答题
-
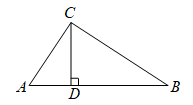
13. 计算: .14. 如图,在 中, ,若 , ,则 上的高 是多少?
 15. 利用平方差公式可以进行简便计算:
15. 利用平方差公式可以进行简便计算:例1:
例2:
请你参考上述例子,运用平方差公式简便计算:
(1)、 ;(2)、 .16. 已知实数 、 、 在数轴上的对应点为 、 、 ,如图所示: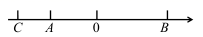
化简: .
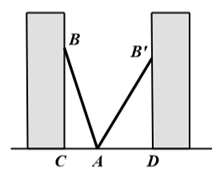
17. 如图有3张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:(1)画一个直角边长为4,面积为6的直角三角形;(2)画一个底边长为4,面积为8的等腰三角形;(3)画一个面积为5的等腰直角三角形;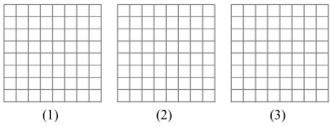 18. 先化简,再求值: ,其中 .19. 已知a= +2,b= -2,求下列代数式的值:(1)、a2b+b2a;(2)、a2-b2.20. 如图,小巷左右两侧是竖直的墙,一架梯子 斜靠在左墙时,梯子底端到左墙角的距离 为0.7米,顶端到地面距离 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离 为2米,求小巷的宽度 .
18. 先化简,再求值: ,其中 .19. 已知a= +2,b= -2,求下列代数式的值:(1)、a2b+b2a;(2)、a2-b2.20. 如图,小巷左右两侧是竖直的墙,一架梯子 斜靠在左墙时,梯子底端到左墙角的距离 为0.7米,顶端到地面距离 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离 为2米,求小巷的宽度 .