福建省南平市延平区2019-2020学年八年级下学期数学线上月考试卷

试卷更新日期：2020-07-29 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.8}$ C、 $\sqrt{5}$ D、 $\sqrt{4}$

查看试题解析
2. 某种流感病毒的直径是 $0.000000085$ 米，这个数据用科学记数法表示为（）

A、 $0.85 \times 10^{- 7}$ B、 $85 \times 10^{- 7}$ C、 $8.5 \times 10^{- 8}$ D、 $8.5 \times 10^{8}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $2 + \sqrt{3} = 2 \sqrt{3}$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
4. 以下列各组数为边长，不能构成直角三角形的是（）

A、5，12，13 B、1，2， $\sqrt{5}$ C、1， $\sqrt{3}$ ，2 D、4，5，6

查看试题解析
5. 已知平行四边形ABCD的周长为56，AB=12，则BC的长为（）

A、4 B、16 C、18 D、24

查看试题解析
6. 如图，数轴上 $M$ ， $N$ ， $P$ ， $Q$ 四点中，能表示 $\sqrt{3}$ 点的是（）

A、 $M$ B、 $N$ C、 $P$ D、 $Q$

查看试题解析
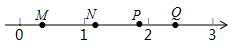7. 已知等腰三角形的一边长等于2，一边长等于4，则它的周长为（）

A、8 B、2 $\sqrt{5}$ C、10 D、8或10

查看试题解析
8. 某服装加工厂加工校服960套的订单，原计划每天做48套．正好按时完成．后因学校要求提前5天交货，为按时完成订单，设每天就多做x套，则x应满足的方程为（）

A、 $\frac{960}{48 + x} - \frac{960}{48} = 5$ B、 $\frac{960}{48} + 5 = \frac{960}{48 + x}$ C、 $\frac{960}{48} - \frac{960}{x} = 5$ D、 $\frac{960}{48} - \frac{960}{48 + x} = 5$

查看试题解析
9. 如图，在 $Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 2$ ，点 $D$ 在 $B C$ 上， $A D = \sqrt{5}$ ， $∠ A D C = 2 ∠ B$ ，则 $B C$ 的长为（）

A、 $\sqrt{5} - 1$ B、 $\sqrt{5} + 1$ C、 $\sqrt{3} - 1$ D、 $\sqrt{3} + 1$

查看试题解析
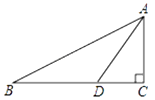10. 如图，正方形ABCD和正方形CGEF的边长分别是2和3，且点B ， C ， G在同一直线上，M是线段AE的中点，连接MF ，则MF的长为（）

A、 $\frac{\sqrt{2}}{4}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析

二、填空题

11. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是.

查看试题解析
12. 因式分解： $2 a^{3} - 4 a^{2} + 2 a =$ ．

查看试题解析
13. 计算： $8 \sqrt{\frac{a}{4}} + \frac{2}{3} \sqrt{9 a} =$ ．

查看试题解析
14. 若菱形的两条对角线长分别是6㎝和8㎝，则该菱形的面积是㎝² ．

查看试题解析
15. 如图，DE是△ABC的中位线，点F在DE上，且∠AFB=90°，AB=6，BC=10，则EF= ．

查看试题解析
16. 已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为．

查看试题解析

三、解答题

17. 计算： ${(\sqrt{3} - 1)}^{0} + | - 2 | - {(\frac{1}{2})}^{- 2}$ ．

查看试题解析
18. 计算：

(1)、 $\sqrt{45} - \sqrt{20} + 5 \sqrt{\frac{1}{5}}$ ；

(2)、 $(2 \sqrt{3} + \sqrt{6}) (2 \sqrt{3} - \sqrt{6})$ ．

查看试题解析
19. 先化简，再求值： $(1 - \frac{2}{x + 1}) \div \frac{x^{2} - 2 x + 1}{x + 1}$ ，其中 $x = 5$ ．

查看试题解析
20. 如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，BD=DC，求证：∠B=∠C

查看试题解析
21. 求证：对角线互相平分的四边形是平行四边形．
小明同学根据题意画出了图形，并写出了已知和求证的一部分，请你补全已知和求证，并写出证明过程：

已知：如图，在四边形ABCD中，AC、BD相交于点O ，．

求证：．

查看试题解析
22. 观察下列等式：
$\frac{2}{\sqrt{3} + 1} = \frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \frac{2 (\sqrt{3} - 1)}{3 - 1} = \sqrt{3} - 1$

$\frac{2}{\sqrt{5} + \sqrt{3}} = \frac{2 (\sqrt{5} - \sqrt{3})}{(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})} = \frac{2 (\sqrt{5} - \sqrt{3})}{{(\sqrt{5})}^{2} - {(\sqrt{3})}^{2}} = \frac{2 (\sqrt{5} - \sqrt{3})}{5 - 3} = \sqrt{5} - \sqrt{3}$

回答下列问题：

(1)、利用你观察到的规律，化简： $\frac{2}{\sqrt{7} + \sqrt{5}}$ ；

(2)、化简： $\frac{2}{\sqrt{2 n + 1} + \sqrt{2 n - 1}}$ ；

(3)、计算： $\frac{2}{\sqrt{3} + 1} + \frac{2}{\sqrt{5} + \sqrt{3}} + \frac{2}{\sqrt{7} + \sqrt{5}} +$ … $+ \frac{2}{\sqrt{75} + \sqrt{73}}$ ．

查看试题解析
23. 如图，在每个小正方形的边长为1的网格中，A ， B ， C均为格点．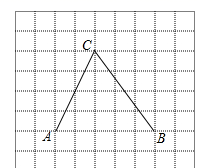

(1)、仅用不带刻度的直尺作BD⊥AC ，垂足为D ，并简要说明道理；

(2)、连接AB ，求△ABC的周长．

查看试题解析
24. 如图，四边形ABCD是矩形，对角线AC的垂直平分线EF交AC于O ，分别交BC、AD于点E、F ．

(1)、求证：四边形AECF是菱形；

(2)、若AB=4，BC=8，求EC的长．

查看试题解析
25. 如图，在正方形ABCD中，E是边AB上的任意一点(不与点A ， B重合)，连接DE ，作点A关于直线DE的对称点为F ，连接EF并延长交BC于点G．

(1)、依题意补全图形，连接DG ，求∠EDG的度数；

(2)、过点E作EH⊥DE交DG的延长线于点H ，连接BH ．线段BH与AE有怎样的数量关系，请写出结论并证明．

查看试题解析