福建省南平市延平区2019-2020学年七年级下学期数学线上月考试卷
试卷更新日期:2020-07-29 类型:月考试卷
一、单选题
-
1. -3的相反数是( )A、-3 B、3 C、 D、2. 与7 是同类项,则a、b、c的值分别为( )A、a=3、b=2、c=1 B、a=3、b=1、c=2 C、a=3、b=2、c=0 D、a=3、b=1、c=03. 下面四个图形中, 与 是对顶角的是( )A、
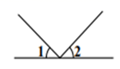 B、
B、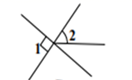 C、
C、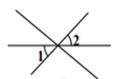 D、
D、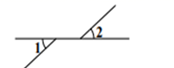 4. 的平方根是( )A、±2 B、2 C、±4 D、45. 下列实数 , , , , , 中无理数有( )A、2个 B、3个 C、4个 D、5个6. 如图,是象棋盘的一部分.若“帅”位于点(1,﹣2)上,“相”位于点(3,﹣2)上,则“炮”位于点( )上.
4. 的平方根是( )A、±2 B、2 C、±4 D、45. 下列实数 , , , , , 中无理数有( )A、2个 B、3个 C、4个 D、5个6. 如图,是象棋盘的一部分.若“帅”位于点(1,﹣2)上,“相”位于点(3,﹣2)上,则“炮”位于点( )上.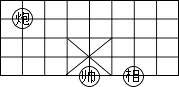 A、(﹣1,1) B、(﹣1,2) C、(﹣2,1) D、(﹣2,2)7. 下列各式中正确的是( )A、 B、 C、 D、8. 如图,a∥b,则下列结论中正确的是( )
A、(﹣1,1) B、(﹣1,2) C、(﹣2,1) D、(﹣2,2)7. 下列各式中正确的是( )A、 B、 C、 D、8. 如图,a∥b,则下列结论中正确的是( )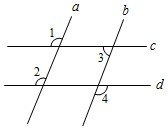 A、∠1=∠2 B、∠2+∠3=180° C、∠1=∠4 D、∠2=49. 在平面直角坐标系xOy中,线段AB的两个点坐标分别为A(﹣1,﹣1),B(1,2).平移线段AB,得到线段A′B′.已知点A′的坐标为(3,1),则点B′的坐标为( )A、(4,4) B、(5,4) C、(6,4) D、(5,3)10. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
A、∠1=∠2 B、∠2+∠3=180° C、∠1=∠4 D、∠2=49. 在平面直角坐标系xOy中,线段AB的两个点坐标分别为A(﹣1,﹣1),B(1,2).平移线段AB,得到线段A′B′.已知点A′的坐标为(3,1),则点B′的坐标为( )A、(4,4) B、(5,4) C、(6,4) D、(5,3)10. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )
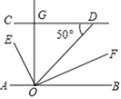 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
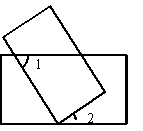
11. 2012年我国各级政府投入医疗卫生领域的资金达8500亿元人民币,850 000 000 000用科学记数法表示为 .12. 3是的立方根;81的平方根是; .13. 如果点P (m+3,m-2)在x轴上,那么点P的坐标 .14. 一个正数x的平方根是2a-3与5-a,则a= .15. 将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2=° .
 16. 如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),点M和点N同时从E(0,2)点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为 .
16. 如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),点M和点N同时从E(0,2)点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为 .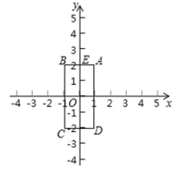
三、解答题
-
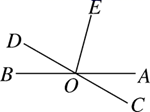
17. 计算: .18. 先化简,再求值: ,其中19. 解方程: .20. 如图,直线AB , CD相交于O , OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.
 21. 如图,△ABC在直角坐标系中.
21. 如图,△ABC在直角坐标系中.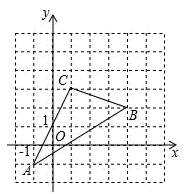 (1)、写出点A,点B的坐标A( , ),B( , );(2)、S△ABC=;(3)、若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1 , 在图中画出△A1B1C1的位置,并写出点A1、B1、C1的坐标.22. 阅读下面的文字,解答问题.
(1)、写出点A,点B的坐标A( , ),B( , );(2)、S△ABC=;(3)、若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1 , 在图中画出△A1B1C1的位置,并写出点A1、B1、C1的坐标.22. 阅读下面的文字,解答问题.大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用 来表示 的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:
(1)、若 的整数部分为 ,小数部分为 ,求 的值.(2)、已知: ,其中 是整数,且 ,求 的值.23. (探究活动)(1)、问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C=( )(等量代换)
即∠B+∠C=∠BEC.
(2)、拓展探究:如果点E运动到图②所示的位置,其他条件不变,试探究∠B、∠C、∠BEC的数量关系并证明;(3)、解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= . (直接写出结论,不用写计算过程)