福建省南平建瓯南河片2019-2020学年七年级下学期数学第一次月考试卷
试卷更新日期:2020-07-29 类型:月考试卷
一、单选题
-
1. 如图所示,∠1和∠2是对顶角的是( )A、
 B、
B、 C、
C、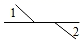 D、
D、 2. 计算 的结果是( )A、 B、2 C、 D、43. 实数-2,0.3, , ,-2π,0.101001000100001中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个4. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
2. 计算 的结果是( )A、 B、2 C、 D、43. 实数-2,0.3, , ,-2π,0.101001000100001中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个4. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )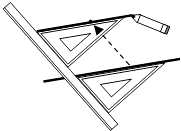 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等5. 估算 的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间6. 方程组 的解为 ,则被遮盖的两个数分别为( )A、5,2 B、1,3 C、2,3 D、4,27. 把点(2,一3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )A、(5,-1) B、(-1,-5) C、(5,-5) D、(-1,-1)8.
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等5. 估算 的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间6. 方程组 的解为 ,则被遮盖的两个数分别为( )A、5,2 B、1,3 C、2,3 D、4,27. 把点(2,一3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )A、(5,-1) B、(-1,-5) C、(5,-5) D、(-1,-1)8.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是( )
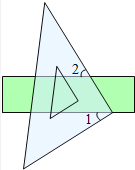 A、32° B、58° C、68° D、60°9. 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
A、32° B、58° C、68° D、60°9. 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( ) A、400cm2 B、500cm2 C、600cm2 D、4000cm210. 定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )A、2 B、3 C、4 D、5
A、400cm2 B、500cm2 C、600cm2 D、4000cm210. 定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )A、2 B、3 C、4 D、5二、填空题
-
11. 如果用(7,3)表示七年级三班,那么八年级二班可表示成 .12. 把命题“等角的补角相等”改写成“如果…那么…”的形式是 .13. 已知 是二元一次方程 kx-2y-1=0 的一组解,则 k= .14. 一个正数的两个平方根分别为a+3和2a+3,则a= .15. 已知点A(4,3),AB∥x轴,且AB=3,则B点的坐标为 .16. 在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , ….若点A1的坐标为(3,1),则点A3的坐标为 , 点A2019的坐标为 .
三、解答题
-
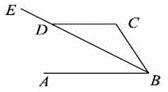
17.(1)、解方程:(2)、计算:(3)、解方程组:18. 如图,AB∥CD,BE平分∠ABC,∠DCB=140°,求∠ABD和∠EDC的度数.
 19. A、B两地相距工40千米,甲、乙两人分别同时从A、B两地出发,相向而行,两小时后两人相遇,然后甲立即返回A地,乙继续前进,当甲回到A地时,乙离A地还有4千米,求甲、乙两人的速度20. 推理填空:
19. A、B两地相距工40千米,甲、乙两人分别同时从A、B两地出发,相向而行,两小时后两人相遇,然后甲立即返回A地,乙继续前进,当甲回到A地时,乙离A地还有4千米,求甲、乙两人的速度20. 推理填空:如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠( )=∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
 21. △ A B C与 在平面直角坐标系中的位置如图.
21. △ A B C与 在平面直角坐标系中的位置如图.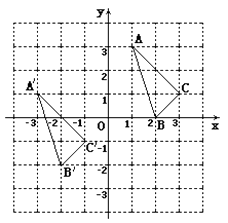 (1)、分别写出下列各点的坐标: ; ; ;(2)、说明 由△ A B C经过怎样的平移得到? .(3)、若点 ( , )是△ A B C内部一点,则平移后 内的对应点 的坐标为;(4)、求△ A B C的面积..22. 如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
(1)、分别写出下列各点的坐标: ; ; ;(2)、说明 由△ A B C经过怎样的平移得到? .(3)、若点 ( , )是△ A B C内部一点,则平移后 内的对应点 的坐标为;(4)、求△ A B C的面积..22. 如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由. 23. 阅读材料:善于思考的小强同学在解方程组 时,采用了一种“整体代换”的解法:
23. 阅读材料:善于思考的小强同学在解方程组 时,采用了一种“整体代换”的解法:解:将方程②变形: ,即 …③,把方程①代入③得: ,y=–1把y=–1代入方程①,得x=4,所以方程组的解为
请你模仿小强同学的“整体代换”法解方程组
24. 小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)、求x和y的值;(2)、商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?