北京首都师大二附2019-2020学年七年级下学期数学月考试卷
试卷更新日期:2020-07-29 类型:月考试卷
一、单选题
-
1. 9的平方根是( )A、 B、 C、 D、32. 若m<0,则点P(3,2m)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各数中的无理数是( )A、 B、 C、 D、4. 如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( )
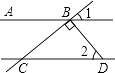 A、40° B、50° C、60° D、140°5. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( )
A、40° B、50° C、60° D、140°5. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( ) A、 B、 C、 D、6. 如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB等于( )
A、 B、 C、 D、6. 如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB等于( ) A、40° B、75° C、85° D、140°7. 若关于x的不等式mx- n>0的解集是 ,则关于x的不等式 的解集是( )A、 B、 C、 D、8. 已知:如图 , ,则 , , 之间的关系是
A、40° B、75° C、85° D、140°7. 若关于x的不等式mx- n>0的解集是 ,则关于x的不等式 的解集是( )A、 B、 C、 D、8. 已知:如图 , ,则 , , 之间的关系是 A、 B、 C、 D、9. 为倡导绿色发展,避免浪费能源,某市准备对居民用电量采用阶梯收费的方法,计划实施三档的阶梯电价:第一档、第二档和第三档的电价分别覆盖全市居民家庭的 , 和 为了合理确定各档之间的界限,相关部门在该市随机调查了20000户居民6月份的用电量 单位: ,并将收集的样本数据进行排序整理 排序样本 ,绘制了如下频数分布直方图 每段用电量均含最小值,不含最大值 .
A、 B、 C、 D、9. 为倡导绿色发展,避免浪费能源,某市准备对居民用电量采用阶梯收费的方法,计划实施三档的阶梯电价:第一档、第二档和第三档的电价分别覆盖全市居民家庭的 , 和 为了合理确定各档之间的界限,相关部门在该市随机调查了20000户居民6月份的用电量 单位: ,并将收集的样本数据进行排序整理 排序样本 ,绘制了如下频数分布直方图 每段用电量均含最小值,不含最大值 .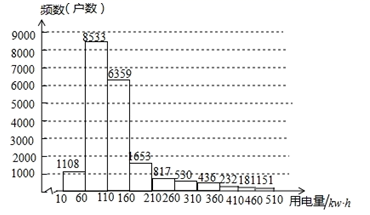
根据统计数据,下面有四个推断:
①抽样调查6月份的用电量,是因为6月份的用电量在一年12个月的用电量中处于中等偏上水平
②在调查的20000户居民中,6月份的用电量的最大值与最小值的差小于500
③月用电量小于 的该市居民家庭按第一档电价交费,月用电量不小于 的该市居民家庭按第三档电价交费
④该市居民家庭月用电量的中间水平 的用户 为
其中合理的是( )
A、①②③ B、①②④ C、①③④ D、②③④10. 在平面直角坐标系中,对于任意三点A , B , C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积” 例如:三点坐标分别为 , , ,则“水平底” ,“铅垂高” ,“矩面积” 若 、 , 三点的“矩面积”为15,则t的值为( )A、 或7 B、 或6 C、 或7 D、 或6二、填空题
-
11. 写出一个比2大且比3小的无理数: .12. 用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 , , .13. 若不等式组 无解,则a的取值范围是 .14. 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为 .
 15. 某手机店今年1-4月的手机销售总额如图1,其中一款音乐手机的销售额占当月手机销售总额的百分比如图2.有以下四个结论:
15. 某手机店今年1-4月的手机销售总额如图1,其中一款音乐手机的销售额占当月手机销售总额的百分比如图2.有以下四个结论:①从1月到4月,手机销售总额连续下降
②从1月到4月,音乐手机销售额在当月手机销售总额中的占比连续下降
③音乐手机4月份的销售额比3月份有所下降
④今年1-4月中,音乐手机销售额最低的是3月
其中正确的结论是(填写序号).
 16. 小字计划在某外卖网站点如下表所示的菜品,已知每份订单的配送费为3元,商家为了促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元,如果小宇在购买下表中所有菜品时,采取适当的下订单方式,那么他点餐的总费用最低可为元.
16. 小字计划在某外卖网站点如下表所示的菜品,已知每份订单的配送费为3元,商家为了促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元,如果小宇在购买下表中所有菜品时,采取适当的下订单方式,那么他点餐的总费用最低可为元.菜品
单价(含包装费)
数量
 水煮牛肉(小)
水煮牛肉(小)30元
1
 醋溜土豆丝(小)
醋溜土豆丝(小)12元
1
 豉汁排骨(小)
豉汁排骨(小)30元
1
 手撕包菜(小)
手撕包菜(小)12元
1
 米饭
米饭3元
2
三、解答题
-
17. 计算: +| ﹣2|+ ﹣(﹣ ).18. 解不等式 ,并把解集在数轴上表示出来.19. 解二元一次方程组:20. 解不等式组21. 阅读下列推理过程,在括号中填写理由.
已知:如图,点D、E分别在线段AB、BC上, , 交BC于点F , AE平分 求证:DF平分
证明: 平分 已知
( )
故 ( )
( )
并且 ( )
( )
平分 ( )
 22. 如图,在平面直角坐标系xOy中, 三个顶点的坐标分别为 , , 将 向右平移5个单位长度,再向下平移4个单位长度,得到 ,其中点 , , 分别为点A , B , C的对应点.
22. 如图,在平面直角坐标系xOy中, 三个顶点的坐标分别为 , , 将 向右平移5个单位长度,再向下平移4个单位长度,得到 ,其中点 , , 分别为点A , B , C的对应点. (1)、请在所给坐标系中画出 ,并直接写出点 的坐标;(2)、若AB边上一点P经过上述平移后的对应点为 ,用含x , y的式子表示点P的坐标; 直接写出结果即可(3)、求 的面积.23. 如图,点 在线段 上,点 在线段 上, , .
(1)、请在所给坐标系中画出 ,并直接写出点 的坐标;(2)、若AB边上一点P经过上述平移后的对应点为 ,用含x , y的式子表示点P的坐标; 直接写出结果即可(3)、求 的面积.23. 如图,点 在线段 上,点 在线段 上, , . (1)、求证: ;(2)、若 于点 , 平分 , ,求 的度数.24. 某年级共有400名学生,为了解该年级学生上学的交通方式,从中随机抽取100名学生进行问卷调查,并对调查数据进行整理、描述和分析,下面给出了部分信息
(1)、求证: ;(2)、若 于点 , 平分 , ,求 的度数.24. 某年级共有400名学生,为了解该年级学生上学的交通方式,从中随机抽取100名学生进行问卷调查,并对调查数据进行整理、描述和分析,下面给出了部分信息A.不同交通方式学生人数分布统计图如下:

B.采用公共交通方式单程所花费时间(分钟)的频数分布直方图如下(数据分成6组: , , , , , );
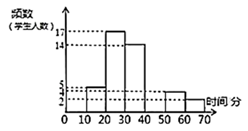
根据以上信息,完成下列问题:
(1)、补全频数分布直方图;(2)、根据不同交通方式学生人数所占的百分比,算出“私家车方式”对应扇形的圆心角是度 .(3)、请你估计全年级乘坐公共交通上学有人,其中单程不少于60分钟的有人.25. 2019年4月29日至2019年10月7日,2019年中国北京世界园艺博览会(简称北京世园会)在中国北京市延庆区举行,展期162天.这是继云南昆明后第二个获得国际园艺生产者协会批准及国际展览局认证授权举办的A1级国际园艺博览会.北京世园会门票种类分为平日票、指定日票、三次票等票种,同时按销售对象分为普通票、优惠票和团队票(学生享受优惠票,15人以上可以享受团体票).指定日包括开园日、“五一”假期、端午节假期、中秋节假期、“十一”假期这些日期,其余时间为平日;三次票是指除指定日外,同一持票人在展会期间可以任选三天入园的票种. 具体如下表:平日票价(元/张)
指定日票价(元/张)
三次票(元/张)
普通票
120
160
300
优惠票
80
100
小明,小亮两家共10人打算一起参观北京世园会(10人均需购票).
(1)、若他们端午节去北京世园会参观购买门票共用去1360元,问买了普通票和优惠票各几张?(2)、如果他们平日去北京世园会参观,且购买门票的费用不超过2000元,那么在保证游玩的前提下最多可以买几张三次票?共有几种买票方案?分别是什么?26. 问题情境:在平面直角坐标系 中有不重合的两点 和点 ,小明在学习中发现,若 ,则 轴,且线段 的长度为 ;若 ,则 轴,且线段 的长度为 ;
(1)、(应用):若点 、 ,则 轴, 的长度为 .
(2)、若点 ,且 轴,且 ,则点 的坐标为 .(3)、(拓展):我们规定:平面直角坐标系中任意不重合的两点 , 之间的折线距离为 ;例如:图1中,点 与点 之间的折线距离为 .
解决下列问题:
如图1,已知 ,若 ,则 ;
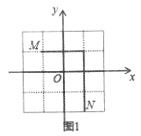 (4)、如图2,已知 , ,若 ,则 .
(4)、如图2,已知 , ,若 ,则 .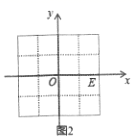 (5)、如图3,已知 的,点 在 轴上,且三角形 的面积为3,则 .
(5)、如图3,已知 的,点 在 轴上,且三角形 的面积为3,则 .