2020年暑期衔接训练青岛版数学八年级下册:第20讲 《一次函数》测试
试卷更新日期:2020-07-29 类型:复习试卷
一、单选题
-
1. 下列函数:(1) y=x ;(2) ;(3) ;(4) ;(5)s=12t;(6)y=30-4x中,是一次函数的有 ( )A、2个 B、3个 C、4个 D、5个2. 已知一次函数y=(m+1)x+m2-1 (m为常数),若图象过原点,则m( )A、m=-1 B、m=±1 C、m=0 D、m=13. 下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是( )A、
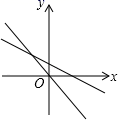 B、
B、 C、
C、 D、
D、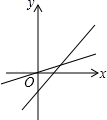 4. 公式
4. 公式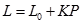 表示当重力为P时的物体作用在弹簧上时弹簧的长度.
表示当重力为P时的物体作用在弹簧上时弹簧的长度. 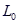 表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( ) A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P5. 图中两直线 , 的交点坐标可以看作方程组( )的解.
表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( ) A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P5. 图中两直线 , 的交点坐标可以看作方程组( )的解. A、 B、 C、 D、6. 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )
A、 B、 C、 D、6. 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )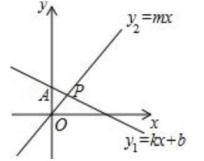 A、1<x< B、1<x< C、1<x< D、1<x<27.
A、1<x< B、1<x< C、1<x< D、1<x<27.如图,在矩形MNPO中(如图1),动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是( )
 A、11 B、15 C、16 D、248.
A、11 B、15 C、16 D、248.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
 A、5个 B、4个 C、3个 D、2个9. 已知平面内有两条直线l1:y=x+2,l2:y=-2x+4交于点A,与x轴分别交于B,C两点,P(m,2m-1)落在△ABC内部(不含边界),则m的取值范围是( )
A、5个 B、4个 C、3个 D、2个9. 已知平面内有两条直线l1:y=x+2,l2:y=-2x+4交于点A,与x轴分别交于B,C两点,P(m,2m-1)落在△ABC内部(不含边界),则m的取值范围是( )
A、-2<m<2 B、 <m< C、0<m< D、-2<m<10. 一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到lh;②A、B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个11. 在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从A地到B地,乙骑自行车从B地到A地,到达A地后立即按原路返回B地.如图是甲、乙两人离B地的距离 与行驶时间 之间的函数图象,下列说法中①A、B两地相距30千米;②甲的速度为15千米/时;③点M的坐标为( ,20);④当甲、乙两人相距10千米时,他们的行驶时间是 小时或 小时. 正确的个数为( )
A、1个 B、2个 C、3个 D、4个11. 在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从A地到B地,乙骑自行车从B地到A地,到达A地后立即按原路返回B地.如图是甲、乙两人离B地的距离 与行驶时间 之间的函数图象,下列说法中①A、B两地相距30千米;②甲的速度为15千米/时;③点M的坐标为( ,20);④当甲、乙两人相距10千米时,他们的行驶时间是 小时或 小时. 正确的个数为( ) A、1个 B、2个 C、3个 D、4个12. 甲、乙两名运动员同时从 地出发前往 地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程 (千米)与行驶时间 (小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时, 或 .其中正确的个数有( )
A、1个 B、2个 C、3个 D、4个12. 甲、乙两名运动员同时从 地出发前往 地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程 (千米)与行驶时间 (小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时, 或 .其中正确的个数有( )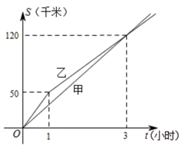 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
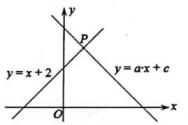
13. 函数 是一次函数,则m= .14. 如图,直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m,3),则方程组 的解为。
 15. 如图,函数 和 的图象相交于点A(m,6),则关于 的不等式 的解集为.
15. 如图,函数 和 的图象相交于点A(m,6),则关于 的不等式 的解集为.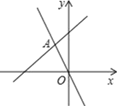 16. 已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为( , ),则不等式组nx-3<kx+1<nx的解集为.17. 已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 .
16. 已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为( , ),则不等式组nx-3<kx+1<nx的解集为.17. 已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 . 18. 一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象.
18. 一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象. (1)、李越骑车的速度为米/分钟;(2)、B点的坐标为;(3)、李越从乙地骑往甲地时,s与t之间的函数表达式为;(4)、王明和李越二人先到达乙地,先到分钟.19. 如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 .
(1)、李越骑车的速度为米/分钟;(2)、B点的坐标为;(3)、李越从乙地骑往甲地时,s与t之间的函数表达式为;(4)、王明和李越二人先到达乙地,先到分钟.19. 如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 . 20. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
20. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 . (把你认为正确说法的序号都填上)

三、解答题
-
21. 已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
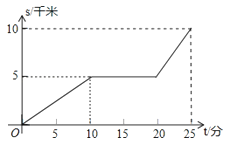
22.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
 23. 如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4 ,
23. 如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4 ,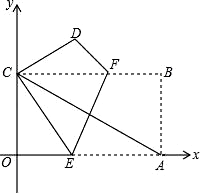 (1)、求AC所在直线的解析式;(2)、将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.(3)、求EF所在的直线的函数解析式.24. (1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(1)、求AC所在直线的解析式;(2)、将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.(3)、求EF所在的直线的函数解析式.24. (1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.

四、综合题
-
25. 某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)、三人间、双人间普通客房各住了多少间?(2)、设三人间共住了x人,则双人间住了人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)、如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?26. 某产品生产车间有工人10名,已知每名工人每天可生产甲种产品10个或乙种产品12个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润150元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.(1)、求出此车间每天获取利润y(元)与x(人)之间的函数关系式;(2)、若要使此车间每天获取利润为14800元,要派多少名工人去生产甲种产品?(3)、若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?27. 在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900 , 且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。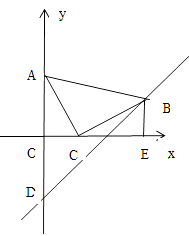 (1)、求证;△AOC≌△CEB(2)、求△ABD的面积。28. 为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地为乙地,在自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地。自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的3倍,如图所示的是自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地的时间x(h)的关系图象,请根据图象提供的信息,回答下列问题:
(1)、求证;△AOC≌△CEB(2)、求△ABD的面积。28. 为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地为乙地,在自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地。自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的3倍,如图所示的是自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地的时间x(h)的关系图象,请根据图象提供的信息,回答下列问题: (1)、自行车队行驶的速度是;邮政车行驶的速度是;a=。(2)、邮政车出发多少小时与自行车队相遇?(3)、当邮政车与自行车队相距15km时,此时离邮政车出发经过了多少小时?
(1)、自行车队行驶的速度是;邮政车行驶的速度是;a=。(2)、邮政车出发多少小时与自行车队相遇?(3)、当邮政车与自行车队相距15km时,此时离邮政车出发经过了多少小时?