河南省郑州市2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期：2020-07-28 类型：期末考试
一、选择题(每小题3分,共 30分)
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 据悉，中科院已经成功攻克了2nm级芯片的一个关键技术，技术的全称为“垂直纳米环栅晶体管”，该项技术完全由我国中科院院士自主研发，获得了多项专利，不但为我国研发2nm芯片打下了一个非常好的基础， 还可能使我国成为世界上第一个拥有2nm芯片的国家，已知2nm=0.000 000 002m ， 0.000 000 002用科学记数法表示为（ ）A、2×10-9 B、2×10-8 C、0.2×10-9 D、0.2×10-83. 下列计算正确的是（ ）A、a6·a4=a24 B、(a3)3=a6 C、(ab4)4=ab4 D、a10÷a9=a4. 如图，直线a//b ， 一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=43°，则∠2的度数为（ ）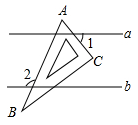
A、101° B、103° C、105° D、107°5. 下面是一些可以自由转动的转盘，按照转出黄色的可能性由大到小进行排列正确的是（ ）
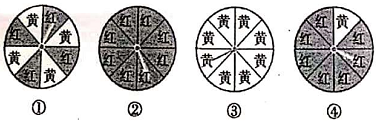A、②④①③ B、①②③④ C、③①④② D、④①③②6. 下面三个图是三个基本作图的作图痕迹.关于三条弧①，②，③，有以下三种说法，
（ 1 ）孤①是以点O为圆心，以任意长为半径所作的弧；
（ 2 ）弧②是以点A为圆心，以任意长为半径所作的弧；
（ 3 ）弧③是以点O为圆心，以大于DE的长为半径所作的弧。
其中正确说法的个数为（ ）
A、3个 B、2个 C、1个 D、0个7. 下列各组条件中，能判定ΔABC≌ΔDEF的是（ ）A、AB=DE ， BC=EF ， ∠A=∠D B、∠A=∠D ， ∠C=∠F ， AC=EF C、∠A=∠D ， ∠B=∠E ， ∠C=∠F D、AB=DE ， BC=EF ， ΔABC的周长＝ΔDEF的周长8. 一个学习小组利用同一块木板，测量了小车从不同高度下滑的时间，他们得到如表数据：支撑物的高度h(cm)
10
20
30
40
50
60
70
80
90
100
小车下滑的时间(s)
4.23
3.00
2.45
2.13
1.89
1.71
1.59
1.50
1.41
1.35
下列说法正确的是（ ）
A、当h=70cm时，t=1.50s B、h每增加10cm ， t减小1.23 C、随着h逐渐变大，也逐渐变大 D、随着h逐渐升高，小车下滑的平均速度逐渐加快9. 七巧板是我国祖先的一项卓越创造，下面四幅图中有三幅图是小明用如图所示的七巧板拼成的，不是用如图所示的七巧板拼成的是（ ）
A、
B、
C、
D、
10. 如图，有两个正方形A ， B ， 现将B放在A的内部得图甲，将A ， B并列放置后构造新的正方形得图乙。若图甲和图乙中阴影部分的面积分别为3和30，则正方形A、B的面积之和为（ ）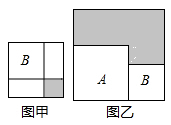
A、33 B、30 C、27 D、24二、填空题（每小题3分，共15分）
-
11. (π－3.14)0－()－2=。12. 如图△ABC≌△EFD ， 请写出一组图中平行的线段。
13. 一天，小明洗手后没有把水龙头拧紧，如果该水龙头每分钟约滴出100滴水，每滴水约0.04毫升，那么所滴出的水的总量y(毫升）与小明离开的时间x（分钟）之间的关系式可以表示为。14. 有一种数字游戏，操作步骤为：第一步，任意写一个自然数（以下简称为原数，原数中至少有一个偶数数字），且位数小于10；第二步，再写一个新三位数，它的百位数字是原数中偶数数字的个数，十位数字是原数中奇数数字的个数，个位数字是原数的位数。以下每一步都以上一步得到的数为原数按照第二步的规则进行重复操作，则重复第二步的操作2020次后得到的数是 。15. 如图，∠AOB=45°，点M、N分别在射线OA、OB上，MN=7，△OMN的面积为14，P是直线MN上的动点，点P关于OA对称的点为P1 ， 点P关于OB对称点为P2 ， 当点P在直线NM上运动时，△OP1 ， P2的面积最小值为。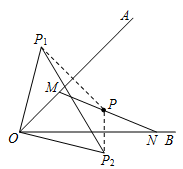
三、解答题（共55分）
-
16. 先化简，再求值。
［(x-y)2-(x+2y)(x-2y)]÷(y),其中x＝2,y= - 。
17. 学习了“简单的轴对称图形”一课后，马老师带领数学兴趣小组的同学来到了校园一角进行探究学习.校园一角的形状如图(1)所示，其中AB ， BC ， CD表示围墙，同学们想通过作角平分线在图示的区域中找一点P(如图(2)所示)，使得点P到三面墙的距离都相等.请你用尺规作图的方法在图(2)中作出点P(不写作法，但要保留作图痕迹)，并解释这样做的道理.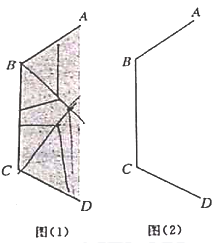
18. 如图，已知点E在BC上，BD⊥AC ， EF⊥AC ， 垂足分别为D、F ， 点M、G在AB上，GF交BD于点H ， ∠BMD+∠ABC=180°，∠1=∠2，则有MD//GF.下面是小颖同学的思考过程，请你在括号内填上依据.
思考过程：
因为BD⊥AC ， EF⊥AC ， 垂足分别为D、F(已知)，
所以∠BDC=90°，∠EFC=90°( ▲ )
所以∠BDC=∠EFC(等量代换)。
所以▲(同位角相等，两直线平行).
所以∠2=∠CBD( ▲)
因为∠1=∠2(已知)，
所以∠1=∠CBD(▲).
所以▲(内错角相等，两直线平行)，
因为∠BMD+∠ABC=180°( ▲)，
所以MD//BC( ▲)
所以MD//GF(▲)
19. 如图，在△ABC中，BD⊥AC于点D ， CE平分∠ACB交AB于点E。∠A=65°，∠CBD=36°，求∠BEC的度数。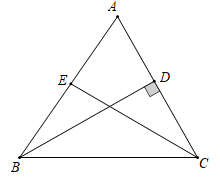
20. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏(扑克牌有四种花色，每种花色有13张)；小明从中任意抽取一张牌(不放回)，小颖从剩余的牌中任意抽取一张，谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为：2，3，4，5，6，7，8，9，10，J ， Q ， K ， A ， 且牌面的大小与花色无关).然后两人把摸到的牌都放回，重新开始游戏·(1)、若小明已经摸到的牌面为2，则小明获胜的概率为 ， 小颖获胜的概率为。(2)、若小明已经摸到的牌面为5，然后小颖摸牌，那么小明和小颖获胜的概率分别是多少?21. 小明骑自行车从家出发去上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校.以下是他本次上学所用的时间t(分)与离家距离S(米)的关系示意图，根据图中提供的信息回答下列问题：
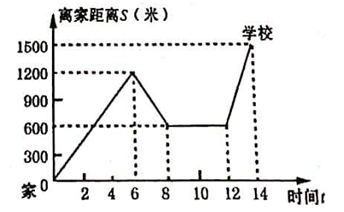(1)、小明家到学校的路程是 米，小明在书店停留了分钟；(2)、在整个上学的途中(哪个时间段)小明骑车速度最快，最快的速度是米/分；(3)、请求出小明从家出发多长时间后，离学校的距离是600米?22. 在学习全等三角形知识时、数学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成。在相对位置变化的同时，始终存在一对全等三角形。通过资料查询，他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下探究：
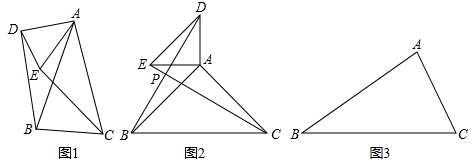(1)、如图1、两个等腰三角形△ABC和△ADE中，AB=AC ， AE=AD ， ∠BAC=∠DAE ， 连接BD、CE、如果把小等腰三角形的腰长看作小手，大等腰三角形的腰长看作大手，两个等腰三角形有公共顶点，类似大手拉着小手，这个就是“手拉手模型”，在这个模型中，和△ADB全等的三角形是 ， 此线BD和CE的数量关系是。(2)、如图2、两个等腰直角三角形△ABC和△ADE中，AB=AC ， AE=AD ， ∠BAC=∠DAE=90°，连接BD ， CE ， 两线交于点P ， 请判断线段BD和CE的数量关系和位置关系，并说明理由：(3)、如图3，已知△ABC、请完成作图：以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等，三个角都等于60°)，连接BE ， CD ， 两线交于点P ， 并直接写出线段BE和CD的数量关系及∠PBC+∠PCB的度数、