河南省南召县2019-2020学年八年级下学期数学期末考试试
试卷更新日期:2020-07-28 类型:期末考试
一、选择题(每小题3分;共30分)
-
1. 下列分式为最简分式的是( )A、 B、 C、 D、2. 若
 ,
, 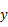 的值均扩大为原来的2倍,则下列分式的值保持不变的是( ) A、 B、 C、 D、3. 下列函数中,y随着 x的减小而增大的是( )A、
的值均扩大为原来的2倍,则下列分式的值保持不变的是( ) A、 B、 C、 D、3. 下列函数中,y随着 x的减小而增大的是( )A、 B、
B、 C、
C、 D、
D、 4. 平行四边形、矩形、菱形、正方形都具有性质的是( )A、对角线互相垂直 B、对角线互相垂直且相等 C、对角线相等 D、对角线互相平分5. 如果 ,那么代数式 的值是( )A、
4. 平行四边形、矩形、菱形、正方形都具有性质的是( )A、对角线互相垂直 B、对角线互相垂直且相等 C、对角线相等 D、对角线互相平分5. 如果 ,那么代数式 的值是( )A、 B、
B、 C、
D、-
6. 如图,已知四边形 ABCD 是平行四边形,下列结论中不正确的是( )
C、
D、-
6. 如图,已知四边形 ABCD 是平行四边形,下列结论中不正确的是( )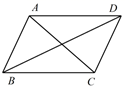 A、当 AB=BC 时,它是菱形 B、当 AC⊥BD 时,它是菱形 C、当 ∠ABC=90° 时,它是矩形 D、当 AC=BD 时,它是正方形7. 在平面直角坐标系中有一点 a(-2,1) ,将点 A 先向右平移3个单位长度,再向下平移 2个单位长度,则平移后点A的坐标为( )A、(1,-3) B、(-5,3) C、(1,-1) D、(-5,-1)8. 四边形 ABCD 中,对角线 AC 、 BD 相交于点 O ,给出下列四个条件:① AD∥BC;② AD=BC ;③ OA=OC ;④ OB=OD .从中任选两个条件,能使四边形 ABCD 为平行四边形的选法有( )A、3 种 B、4种 C、5种 D、6种9. 若数
A、当 AB=BC 时,它是菱形 B、当 AC⊥BD 时,它是菱形 C、当 ∠ABC=90° 时,它是矩形 D、当 AC=BD 时,它是正方形7. 在平面直角坐标系中有一点 a(-2,1) ,将点 A 先向右平移3个单位长度,再向下平移 2个单位长度,则平移后点A的坐标为( )A、(1,-3) B、(-5,3) C、(1,-1) D、(-5,-1)8. 四边形 ABCD 中,对角线 AC 、 BD 相交于点 O ,给出下列四个条件:① AD∥BC;② AD=BC ;③ OA=OC ;④ OB=OD .从中任选两个条件,能使四边形 ABCD 为平行四边形的选法有( )A、3 种 B、4种 C、5种 D、6种9. 若数 使关于
使关于  的分式方程 的解为正数,则
的分式方程 的解为正数,则  的取值正确的是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中有一边长为
的取值正确的是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中有一边长为 的正方形
的正方形 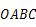 ,边
,边  ,
,  分别在
分别在  轴、
轴、 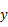 轴上,如果以对角线
轴上,如果以对角线  为边作第二个正方形
为边作第二个正方形  ,再以对角线
,再以对角线  为边作第三个正方形
为边作第三个正方形  ,照此规律作下去,则点 的坐标为( )
,照此规律作下去,则点 的坐标为( )  A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分;共15分)
-
11. .12. 分式方程 的解为.13. 如图,矩形ABCD中,AB=6,BC=3,连接AC , 分别以点A和点C为圆心,大于 的长为半径作弧,两弧相交于点M , N , 作直线MN , 分别交CD、AB于点E、F , 连接AE、CF , 则四边形AECF的周长是 .
 14. 如图,点
14. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点
是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点  ,以
,以  为边作平行四边形
为边作平行四边形  ,其中
,其中  、
、  在
在  轴上,则
轴上,则  为.
为.  15. 如图,直角坐标系中的网格由单位正方形构成,已知△ABC , A(2,3),B(-2,0),C(0,-1).若以A , B , C , D为顶点的四边形为平行四边形,则点D的坐标为 .
15. 如图,直角坐标系中的网格由单位正方形构成,已知△ABC , A(2,3),B(-2,0),C(0,-1).若以A , B , C , D为顶点的四边形为平行四边形,则点D的坐标为 .
三、解答题(8+9+9+9+9+10+10+11=75分)
-
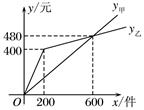
16. 先化简,再求值 ,其中 满足关于x的不等式组 的整数解.17. 某厂家在甲、乙两家商场销售同一种商品所获得的利润分别为y甲 , y乙(单位:元),y甲 , y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象分别求出y甲 , y乙关于x的函数解析式.
 18. 如图,四边形
18. 如图,四边形 为矩形,以点
为矩形,以点  为原点建立直角坐标系,点
为原点建立直角坐标系,点  在
在  轴的负半轴上,点
轴的负半轴上,点  在
在 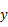 轴的正半轴上,已知点
轴的正半轴上,已知点  坐标为(
坐标为( 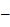 2,4),反比例函数 图象经过 BC 的中点
2,4),反比例函数 图象经过 BC 的中点 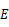 ,且与 AB 交于点
,且与 AB 交于点  .
.
 (1)、求
(1)、求 的值; (2)、设直线
的值; (2)、设直线 为 ,求 的解析式; (3)、直接写出: > 时,x的取值范围.19. 如图,在矩形ABCD中,AB=8,BC=10,E为CD边上一点,将△ADE沿AE折叠,使点D落在BC边上的点F处.
为 ,求 的解析式; (3)、直接写出: > 时,x的取值范围.19. 如图,在矩形ABCD中,AB=8,BC=10,E为CD边上一点,将△ADE沿AE折叠,使点D落在BC边上的点F处. (1)、求BF的长;(2)、求CE的长.20. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连接CD、BE .
(1)、求BF的长;(2)、求CE的长.20. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连接CD、BE . (1)、求证:CE=AD;(2)、①当AD=DB时,四边形BECD的形状为;
(1)、求证:CE=AD;(2)、①当AD=DB时,四边形BECD的形状为;②在①的条件下,当∠A=度时,四边形BECD是正方形.
21. 某商店销售 台
台  型和
型和  台
台  型电脑的利润为
型电脑的利润为  元,销售
元,销售  台
台  型和
型和  台
台  型电脑的利润为
型电脑的利润为  元.
(1)、求每台
元.
(1)、求每台 型电脑和
型电脑和  型电脑的销售利润;
(2)、该商店计划一次购进两种型号的电脑共
型电脑的销售利润;
(2)、该商店计划一次购进两种型号的电脑共 台,其中
台,其中  型电脑的进货量不超过
型电脑的进货量不超过  型电脑的
型电脑的  倍.设购进
倍.设购进  型电脑
型电脑  台,这
台,这  台电脑的销售总利润为
台电脑的销售总利润为  元.
元. ①直接写出:
 与
与  的函数关系式 ▲;
的函数关系式 ▲;②该商店购进
 型、
型、  型各多少台,才能使销售利润最大?最大利润是多少?22. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:
型各多少台,才能使销售利润最大?最大利润是多少?22. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:x
…
-3
-2
-1
0
1
2
3
…
y
…
1
2
1
0
1
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
 (1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象.(2)、研究函数并结合图象与表格,回答下列问题:
(1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象.(2)、研究函数并结合图象与表格,回答下列问题:①点A(-5,y1),B( ,y2)在函数图象上,则y1y2(填“>”,“=”或“<”)
②点C(x1 , 5),D(x2 , )也在函数图象上,则x1x2;(填“>”,“=”或“<”)
③当函数值y=2时,自变量x的值为;
④若直线y=a与函数图象有三个不同的交点,则a的取值范围为 .
23. 如图,直线 分别与 轴、
轴、  轴交于
轴交于  ,
,  两点,与直线 交于点
两点,与直线 交于点  .
.  (1)、b=;k=;点
(1)、b=;k=;点 坐标为; (2)、在线段AB上有一动点
坐标为; (2)、在线段AB上有一动点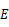 ,过点
,过点 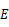 作
作  轴的平行线交直线y2于点
轴的平行线交直线y2于点  ,设点
,设点 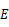 的横坐标为
的横坐标为  ,当
,当  为何值时,以
为何值时,以  、B、E、F为顶点的四边形是平行四边形;
(3)、若点
、B、E、F为顶点的四边形是平行四边形;
(3)、若点 为
为  轴上一点,则在平面直角坐标系中是否存在一点
轴上一点,则在平面直角坐标系中是否存在一点  ,使得
,使得  ,
,  ,
,  ,
, 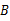 四个点能构成一个菱形.若存在,直接写出所有符合条件的
四个点能构成一个菱形.若存在,直接写出所有符合条件的  点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.