云南省红河州蒙自市2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、填空题
-
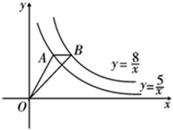
1. 数-2020的绝对值是 .2. 已知分式 有意义,则x的取值范围是 .3. 计算: .4. 关于x的一元二次方程x2+3x+k=0没有实数根,则k的值可以是 . (填一个值即可)5. 如图,点 A 在双曲线y= 上,点 B 在双曲线y= 上,且AB∥x轴,则△OAB 的面积等于 .
 6. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2 、O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 个单位长度,则第2020秒时,点P的坐标是 .
6. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2 、O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 个单位长度,则第2020秒时,点P的坐标是 .
二、选择题
-
7. 我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为( )A、7.5x105 B、7.5×10-5 C、0.75×10-4 D、75×10-68. 下列运算或变形正确的是( )A、﹣2a+2b=﹣2(a+b) B、(2a2)3=6a6 C、a3+4a=5a3 D、3a2•2a3=6a59. 如图是由5个完全相同的小正方形搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
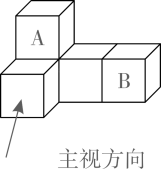 A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变10. 已知一组数据5,8,8,9,10,以下说法错误的是( )A、平均数是8 B、众数是8 C、中位数是8 D、方差是811. 不等式组 的解集在数轴上表示正确的是( )A、
A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变10. 已知一组数据5,8,8,9,10,以下说法错误的是( )A、平均数是8 B、众数是8 C、中位数是8 D、方差是811. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 12. 已知点 在同一个函数的图象上,这个函数可能是( )A、 B、 C、 D、13. 如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
12. 已知点 在同一个函数的图象上,这个函数可能是( )A、 B、 C、 D、13. 如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )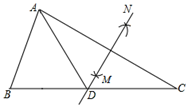 A、65° B、60° C、55° D、45°14. 如图, 中, , , ,则阴影部分的面积是( )
A、65° B、60° C、55° D、45°14. 如图, 中, , , ,则阴影部分的面积是( )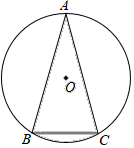 A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
15. 先化简,再求值: , 其中x=-4.16. 有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
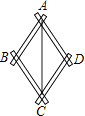 17. 张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).
17. 张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整). (1)、抽取的这部分男生有_▲_人,请补全频数分布直方图;(2)、抽取的这部分男生成绩的中位数落在组?扇形统计图中D组对应的圆心角是多少度?(3)、如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?18. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.(1)、求该店有客房多少间?房客多少人?(2)、假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?19.
(1)、抽取的这部分男生有_▲_人,请补全频数分布直方图;(2)、抽取的这部分男生成绩的中位数落在组?扇形统计图中D组对应的圆心角是多少度?(3)、如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?18. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.(1)、求该店有客房多少间?房客多少人?(2)、假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?19.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
 (1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.20. 小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.21. 如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD、BC相交于点E.
(1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.20. 小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.21. 如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD、BC相交于点E.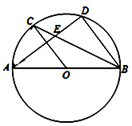 (1)、求证: ;(2)、若CE=1,BE=3,求⊙O的半径.22. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0),B(1,0)两点,与y轴交于点C,其顶点为D,连接AD,点P是线段AD上一个动点(不与A,D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)、求证: ;(2)、若CE=1,BE=3,求⊙O的半径.22. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0),B(1,0)两点,与y轴交于点C,其顶点为D,连接AD,点P是线段AD上一个动点(不与A,D重合),过点P作y轴的垂线,垂足点为E,连接AE. (1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如果P点的坐标为(x , y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值.23. 定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
(1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如果P点的坐标为(x , y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值.23. 定义:有一组邻边相等且对角互补的四边形叫做等补四边形. (1)、理解:
(1)、理解:如图1,点 在 上, 的平分线交 于点D,连接 求证:四边形 是等补四边形;
(2)、探究:如图2,在等补四边形 中 连接 是否平分 请说明理由.
(3)、运用:如图3,在等补四边形 中, ,其外角 的平分线交 的延长线于点 求 的长.