陕西省铜川市新区2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、 B、 C、 D、2. 如图,下面几何体是由一个圆柱被经过上下底面圆心的平面截得的,则它的左视图是( )
 A、
A、 B、
B、 C、
C、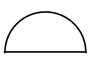 D、
D、 3. 如图,若 , 则图中与 互补的角有( )
3. 如图,若 , 则图中与 互补的角有( ) A、1个 B、2个 C、3个 D、4个4. 点 在正比例函数 的图像上,若 ,则 的值是( )A、15 B、8 C、-15 D、-85. 若 , 则下列运算正确的是( )A、 B、 C、 D、6. 如图,在四边形 中,对角线AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )
A、1个 B、2个 C、3个 D、4个4. 点 在正比例函数 的图像上,若 ,则 的值是( )A、15 B、8 C、-15 D、-85. 若 , 则下列运算正确的是( )A、 B、 C、 D、6. 如图,在四边形 中,对角线AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( ) A、1对 B、2对 C、3对 D、4对7. 若直线 经过点 ,且与y轴的交点在x轴上方,则k的取值范围是( )A、 B、 C、 D、8. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( )
A、1对 B、2对 C、3对 D、4对7. 若直线 经过点 ,且与y轴的交点在x轴上方,则k的取值范围是( )A、 B、 C、 D、8. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( ) A、 B、 C、 D、9. 如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )
A、 B、 C、 D、9. 如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )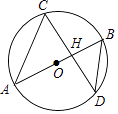 A、 B、 C、 D、10. 若一个二次函数 的图像经过两点 ,则下列关系正确的是( )A、 B、 C、 D、
A、 B、 C、 D、10. 若一个二次函数 的图像经过两点 ,则下列关系正确的是( )A、 B、 C、 D、二、填空题
-
11. 在实数-5, 中,最小的一个无理数是.12. 已知正六边形的边长为8,则较短的对角线长为.13. 如图, 的三个顶点分别为 .若反比例函数 在第一象限内的图象与 有交点,则 的取值范围是.
 14. 已知正方形 的边长为6,点 , 分别在 , 上, , 与 相交于点 ,点 为 的中点,连接 ,则 的长为.
14. 已知正方形 的边长为6,点 , 分别在 , 上, , 与 相交于点 ,点 为 的中点,连接 ,则 的长为.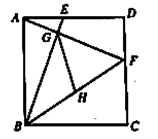
三、解答题
-
15. 计算:16. 解分式方程:17. 如图,已知在正方形ABCD中,M是BC边上一定点,连接AM,请用尺规作图法,在AM上求作一点P,使得△DPA∽△ABM(不写做法保留作图痕迹)
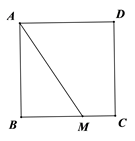 18. 如图,点D在等边 的边 上,作 ,交 于点G,点F在边 上,连接 并延长,交 的延长线于点E,且 .求证: .
18. 如图,点D在等边 的边 上,作 ,交 于点G,点F在边 上,连接 并延长,交 的延长线于点E,且 .求证: . 19. 随着社会的发展,物质生活极大丰富,青少年的营养过剩,身体越来越胖,某校为了了解八年级学生的体重情况,随机抽取了八年级部分学生进行调查,将抽取学生的体重情况绘制成如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
19. 随着社会的发展,物质生活极大丰富,青少年的营养过剩,身体越来越胖,某校为了了解八年级学生的体重情况,随机抽取了八年级部分学生进行调查,将抽取学生的体重情况绘制成如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:组别
体重(千克}
人数
A
3
B
12
C
a
D
10
E
8
F
2
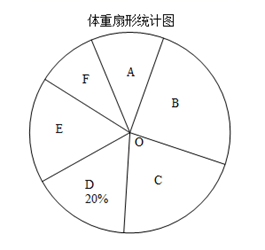 (1)、求得 (直接写出结果); 在扇形统计图中,D组所在扇形的圆心角的度数等于 ;(2)、调查的这组数据的中位数落在组;(3)、如果体重不低于55千克,属于偏胖,该校八年级有1200名学生,请估算该年级体重偏胖的学生大约有多少人?20. 汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)
(1)、求得 (直接写出结果); 在扇形统计图中,D组所在扇形的圆心角的度数等于 ;(2)、调查的这组数据的中位数落在组;(3)、如果体重不低于55千克,属于偏胖,该校八年级有1200名学生,请估算该年级体重偏胖的学生大约有多少人?20. 汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)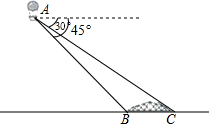 21. 为了优化环境,将对某一小区环境进行绿化,现有甲、乙两家绿化公司进行了投标,各自推出了绿化收费方案如下:甲公司绿化费用y(元) 与绿化面积x(平方米)是一次函数关系,如图所示。
21. 为了优化环境,将对某一小区环境进行绿化,现有甲、乙两家绿化公司进行了投标,各自推出了绿化收费方案如下:甲公司绿化费用y(元) 与绿化面积x(平方米)是一次函数关系,如图所示。
乙公司:绿化面积不超过1000平方米时,统一收取费用5000元;绿化面积超过1000平方米时,超过部分每平方米收取3元.
(1)、求甲、乙公司绿化费用y(元)与绿化面积x(平方米)的函数表达式;(2)、如果该小区目前的绿化面积是1500平方米,试通过计算说明:选择哪家公司的绿化费用较少?22. 西安市历史文化底蕴深厚,旅游资源丰富,钟楼、大雁塔兵马俑三个景点是人们节假日游玩的热门景点(1)、李辉从这三个景点中随机选取一个景点去游玩,求他去钟楼的概率;(2)、张慧、王丽两名同学,各自从三个景点中随机选取一个作为周末游玩的景点,用树状图或列表法求他们同时选中大雁塔的概率.23. 如图, 为 的直径,F为弦 的中点,连接 并延长与 交于点D,过点D作 的切线,交 的延长线于点E. (1)、求证: ;(2)、连接 ,若 ,请求出四边形 的面积。24. 如图,曲线 是抛物线的一部分,与x轴交于 两点,与y轴交于点C,且表达式 ,曲线 与曲线 关于直线 对称.
(1)、求证: ;(2)、连接 ,若 ,请求出四边形 的面积。24. 如图,曲线 是抛物线的一部分,与x轴交于 两点,与y轴交于点C,且表达式 ,曲线 与曲线 关于直线 对称. (1)、求 三点的坐标和曲线 的表达式;(2)、过点C作 轴交曲线 于点D,连结 ,在曲线 .上有一点M,使得四边形 为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标.25. 如图
(1)、求 三点的坐标和曲线 的表达式;(2)、过点C作 轴交曲线 于点D,连结 ,在曲线 .上有一点M,使得四边形 为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标.25. 如图
问题提出
(1)、如图①,在等腰Rt△ABC中,斜边AC=4,点D为AC上一点,连接BD,则BD的最小值为;(2)、如图②,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,求AD的最小值;(3)、如图③,四边形ABCD是规划中的休闲广场示意图,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2 km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.