辽宁省沈阳市大东区2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、5 B、-5 C、- D、2. 如图是由6个棱长均为1的正方体组成的几何体,从左面看到的该几何体的形状为( )
 A、
A、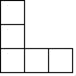 B、
B、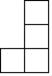 C、
C、 D、
D、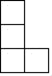 3. 下列图形中,不是中心对称图形的是( )A、平行四边形 B、矩形 C、菱形 D、等边三角形4. 据不完全统计,截至2月12日,河南省已有79家外商投资企业为抗击“新冠肺炎”疫情捐赠总价值约2.61亿元的物资和现金.数据“2.61亿”用科学记数法表示为( )A、 B、 C、 D、5. 数据4,3,2,1,3的众数是( )A、4 B、3 C、2 D、16. 若分式 的值为0,则x的值是( )
3. 下列图形中,不是中心对称图形的是( )A、平行四边形 B、矩形 C、菱形 D、等边三角形4. 据不完全统计,截至2月12日,河南省已有79家外商投资企业为抗击“新冠肺炎”疫情捐赠总价值约2.61亿元的物资和现金.数据“2.61亿”用科学记数法表示为( )A、 B、 C、 D、5. 数据4,3,2,1,3的众数是( )A、4 B、3 C、2 D、16. 若分式 的值为0,则x的值是( )
A、2或﹣2 B、2 C、﹣2 D、07. 下列事件中,是必然事件的是( )A、掷一次骰子,向上一面的点数是6 B、经过有交通信号灯的路口,遇到红灯 C、射击运动员射击一次,命中靶心 D、13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月8. 如图,BC⊥DE,垂足为点C,AC∥BD,∠B=40°,则∠ACE的度数为( ) A、40° B、50° C、45° D、60°9. 不等式组 的解集为( )A、6≤x<8 B、6<x≤8 C、2≤x<4 D、2<x≤810. 南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A、40° B、50° C、45° D、60°9. 不等式组 的解集为( )A、6≤x<8 B、6<x≤8 C、2≤x<4 D、2<x≤810. 南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )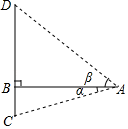 A、asinα+asinβ B、acosα+acosβ C、atanα+atanβ D、
A、asinα+asinβ B、acosα+acosβ C、atanα+atanβ D、二、填空题
-
11. 一枚材质均匀的骰子,六个面的点数分别是1,2,3,4,5,6,投这个骰子,掷的的点数大于4的概率是.12. 在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则 的值是.13. 已知关于x的方程x2﹣2kx+4=0有两个相等的实数根,则k的取值是.14. 已知正比例函数y=2x与反比例函数y= (m为常数)的一个交点为A,过点A作x轴的垂线,垂足为B,且OB=3,则m的值.15. 如图,在△ABC中,∠ACB=90°,AC=BC=2,D是边AC的中点,CE⊥BD于E.若F是边AB上的点,且使△AEF为等腰三角形,则AF的长为.

三、解答题
-
16. 计算:(2020﹣π)0﹣2cos30°+ +(﹣ )﹣1.17. 如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上,AG=CH,过O作直线EF,与边AB,CD分别相交于点E,F.求证:四边形EHFG是平行四边形.
 18. 一个不透明的盒子中装有两个红球,一个白球和一个黄球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,请你用列表法或画树状图法求两次摸到的球的颜色都是红色的概率.19. 某校为了解学生课外阅读情况,就学生每周阅读时间线上随机调查了部分学生,调查结果整理如下:
18. 一个不透明的盒子中装有两个红球,一个白球和一个黄球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,请你用列表法或画树状图法求两次摸到的球的颜色都是红色的概率.19. 某校为了解学生课外阅读情况,就学生每周阅读时间线上随机调查了部分学生,调查结果整理如下:阅读时间人数统计表
阅读时间t(小时)
人数
占人数百分比
0≤t<0.5
4
20%
0.5≤t<1
m
15%
1≤t<1.5
5
25%
1.5≤t<2
6
n
2≤t<2.5
2
10%
根据图表解答下列问题:
(1)、此次抽样调查中,共抽取了名学生;(2)、在阅读时间人数统计表中m= , n=;(3)、根据抽样调查的结果,请估计该校2000名学生中有多少名学生每天阅读时间在2≤t<2.5时间段?20. 某村组织村民种植香菇,2017年的人均收入为40000元,由于此项种植技术得到很好指导,2019年的人均收入为48400元.(1)、求2017年到2019年该村人均收入的年平均增长率;(2)、假设2020年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2020年该村的人均收入是多少元?21. 如图,已知AB是⊙O的直径,C是⊙O上一点,连接AC,BC.OE∥BC交AC于E,过点A作⊙O的切线交OE的延长线于点D,连接DC并延长交AB的延长线于点F. (1)、求证:DC是⊙O的切线;(2)、若∠BAC=30°,AB=4,直接写出线段CF的长.22. 如图,Rt△OAB的直角边OA在x轴上,边OB在y轴上,A的坐标为(6,0),B的坐标为(0,3),在第一象限有一点C的坐标为(3,4).
(1)、求证:DC是⊙O的切线;(2)、若∠BAC=30°,AB=4,直接写出线段CF的长.22. 如图,Rt△OAB的直角边OA在x轴上,边OB在y轴上,A的坐标为(6,0),B的坐标为(0,3),在第一象限有一点C的坐标为(3,4). (1)、求直线AB的函数表达式;(2)、P是x轴上一动点,点P在运动过程中,是否存在某个位置,使得∠PBO=∠BOC?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、若动点P在x轴上从点(﹣6,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.请直接写出当t为何值时,在直线l上存在点M,在直线AB上存在点Q.使得以OC为一边,O,C,M,Q为顶点的四边形为菱形.23. 在正方形ABCD中,AB=6,对角线AC和BD相交于点O,E是AB所在直线上一点(不与点B重合),将线段OE绕点E顺时针旋转90°得到EF.
(1)、求直线AB的函数表达式;(2)、P是x轴上一动点,点P在运动过程中,是否存在某个位置,使得∠PBO=∠BOC?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、若动点P在x轴上从点(﹣6,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.请直接写出当t为何值时,在直线l上存在点M,在直线AB上存在点Q.使得以OC为一边,O,C,M,Q为顶点的四边形为菱形.23. 在正方形ABCD中,AB=6,对角线AC和BD相交于点O,E是AB所在直线上一点(不与点B重合),将线段OE绕点E顺时针旋转90°得到EF. (1)、如图1,当点E和点A重合时,连接BF,直接写出BF的长为;(2)、如图2,点E在线段AB上,且AE=1,连接BF,求BF的长;(3)、若DG:AG=2:1,连接CF,H是CF的中点,是否存在点E使△GEH是以EG为直角边的直角三角形?若存在,请直接写出EB的长;若不存在,试说明理由.24. 如图1,二次函数y=﹣x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l是抛物线的对称轴,D是抛物线的顶点.
(1)、如图1,当点E和点A重合时,连接BF,直接写出BF的长为;(2)、如图2,点E在线段AB上,且AE=1,连接BF,求BF的长;(3)、若DG:AG=2:1,连接CF,H是CF的中点,是否存在点E使△GEH是以EG为直角边的直角三角形?若存在,请直接写出EB的长;若不存在,试说明理由.24. 如图1,二次函数y=﹣x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l是抛物线的对称轴,D是抛物线的顶点. (1)、求该抛物线的函数表达式;(2)、如图1,连结BD,线段OC上点E关于直线l的对称点E'恰好在线段BD上,求点E的坐标;(3)、如图2,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线分别与BC交于点M,与x轴交于点N.试问:抛物线上是否存在点Q,使得△PQN与△AMN的面积相等,且线段PQ的长度最小?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
(1)、求该抛物线的函数表达式;(2)、如图1,连结BD,线段OC上点E关于直线l的对称点E'恰好在线段BD上,求点E的坐标;(3)、如图2,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线分别与BC交于点M,与x轴交于点N.试问:抛物线上是否存在点Q,使得△PQN与△AMN的面积相等,且线段PQ的长度最小?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.