江苏省盐城市2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 过点P画 的垂线,三角尺的放法正确的是( )A、
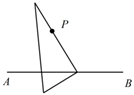 B、
B、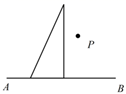 C、
C、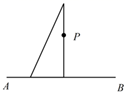 D、
D、 2. 的结果是( )A、-6 B、6 C、-8 D、83. 下列计算结果正确的是( )A、 B、 C、 D、4. 下列等式不成立的是( )A、 B、 C、 D、5. 在四边形 中,对角线 互相平分,若添加一个条件使得四边形 是菱形,则这个条件可以是( )A、 B、 C、 D、 ∥6. 若关于x的不等式组的解在数轴上如图所示,则这个不等式组的解是( )
2. 的结果是( )A、-6 B、6 C、-8 D、83. 下列计算结果正确的是( )A、 B、 C、 D、4. 下列等式不成立的是( )A、 B、 C、 D、5. 在四边形 中,对角线 互相平分,若添加一个条件使得四边形 是菱形,则这个条件可以是( )A、 B、 C、 D、 ∥6. 若关于x的不等式组的解在数轴上如图所示,则这个不等式组的解是( ) A、 B、 C、 D、7. 如图,点A在双曲线 上,点B在双曲线 上,C、D 在x轴上,若四边形 为矩形,则它的面积为( )
A、 B、 C、 D、7. 如图,点A在双曲线 上,点B在双曲线 上,C、D 在x轴上,若四边形 为矩形,则它的面积为( ) A、1 B、2 C、3 D、48. 某市初中毕业生进行了一项技能测试,有4万名考生的得分都是不小于70的两位数,从中随机抽取4000个数据,统计如下表:
A、1 B、2 C、3 D、48. 某市初中毕业生进行了一项技能测试,有4万名考生的得分都是不小于70的两位数,从中随机抽取4000个数据,统计如下表:数据x
70≤x≤79
80≤x≤89
90≤x≤99
个数
800
2000
1200
平均数
78
85
92
请根据表格中的信息,估计这4万个数据的平均数约为( )
A、92.1 B、85.7 C、83.4 D、78.8二、填空题
-
9. 的倒数是 .10. 在一次考试中,某小组8名同学的成绩(单位:分)分别是:7,10,9,8,7,9,9,8, 则这组数据的众数是.11. 一种细菌的半径是 ,则用小数可表示为 .12. 在 中, , ,点D在 边上,且 ,则 =.
 13. 如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC=°.
13. 如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC=°.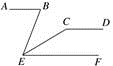 14. 已知方程 的一个根是2,这个方程的另一个根是.15. 有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为.
14. 已知方程 的一个根是2,这个方程的另一个根是.15. 有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为. 16. 如图,在四边形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=12,E是AB上一点,且∠GCE=45°,BE=4,则GE=.
16. 如图,在四边形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=12,E是AB上一点,且∠GCE=45°,BE=4,则GE=.
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 , .19. 如图,△ABC在方格中.

①请在方格纸上建立平面直角坐标系,使A、C两点坐标依次为 (1,2)、 (3,1),并写出点B坐标为 ▲ ;
②以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形.
20. 如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况. (1)、最低气温的中位数是℃;3月24日的温差是℃;(2)、分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;(3)、经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?21. 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC是120米,求河宽CD的长?
(1)、最低气温的中位数是℃;3月24日的温差是℃;(2)、分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;(3)、经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?21. 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC是120米,求河宽CD的长? 22. 如图,管中放置着三根同样的绳子AA1、BB1、CC1;
22. 如图,管中放置着三根同样的绳子AA1、BB1、CC1; (1)、小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?(2)、小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.23. 如图,反比例函数 的图象过等边三角形 的顶点 ,已知点B在x轴上.
(1)、小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?(2)、小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.23. 如图,反比例函数 的图象过等边三角形 的顶点 ,已知点B在x轴上. (1)、求反比例函数的表达式;(2)、若要使点B在上述反比例函数的图象上,需将 向上平移多少个单位长度?24. 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)、求反比例函数的表达式;(2)、若要使点B在上述反比例函数的图象上,需将 向上平移多少个单位长度?24. 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. (1)、求证:PB是⊙O的切线;(2)、连接OP,若OP∥BC,且OP=8,⊙O的半径为2 , 求BC的长.25. 某饰品店老板去批发市场购买新款手链,第一次购手链共用1000元,将该手链以每条定价28元销售,并很快售完,所得利润率高于30%.由于该手链深得年轻人喜爱,十分畅销,第二次去购进手链时,每条的批发价已比第一次高5元,共用去了1500元,所购数量比第一次多10条.当这批手链以每条定价32元售出80%时,出现滞销,便以5折价格售完剩余的手链.现假设第一次购进手链的批发价为x元/条.(1)、用含x的代数式表示:第一次购进手链的数量为条;(2)、求x的值;(3)、不考虑其他因素情况下,试问该老板第二次售手链是赔钱了,还是赚钱了?若赔钱,赔多少?若赚钱,赚多少?26. 已知△ABC是边长为 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)、求证:PB是⊙O的切线;(2)、连接OP,若OP∥BC,且OP=8,⊙O的半径为2 , 求BC的长.25. 某饰品店老板去批发市场购买新款手链,第一次购手链共用1000元,将该手链以每条定价28元销售,并很快售完,所得利润率高于30%.由于该手链深得年轻人喜爱,十分畅销,第二次去购进手链时,每条的批发价已比第一次高5元,共用去了1500元,所购数量比第一次多10条.当这批手链以每条定价32元售出80%时,出现滞销,便以5折价格售完剩余的手链.现假设第一次购进手链的批发价为x元/条.(1)、用含x的代数式表示:第一次购进手链的数量为条;(2)、求x的值;(3)、不考虑其他因素情况下,试问该老板第二次售手链是赔钱了,还是赚钱了?若赔钱,赔多少?若赚钱,赚多少?26. 已知△ABC是边长为 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.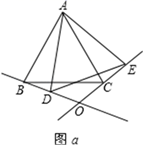
 (1)、如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;(2)、当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;(3)、在θ从60°到120°的旋转过程中,点O运动的轨迹长为.27. 如图1,已知抛物线 与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
(1)、如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;(2)、当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;(3)、在θ从60°到120°的旋转过程中,点O运动的轨迹长为.27. 如图1,已知抛物线 与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D. (1)、求点D的坐标和直线BC对应的一次函数关系式;(2)、若正方形PQMN的一边PQ在线段AB上,另两个顶点M、N分别在BC、AC上,试求M、N两点的坐标;(3)、如图1,E是线段BC上的动点,过点E作DE的垂线交BD于点F,求DF的最小值.
(1)、求点D的坐标和直线BC对应的一次函数关系式;(2)、若正方形PQMN的一边PQ在线段AB上,另两个顶点M、N分别在BC、AC上,试求M、N两点的坐标;(3)、如图1,E是线段BC上的动点,过点E作DE的垂线交BD于点F,求DF的最小值.