江苏省苏州市姑苏区2020年数学中考一模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 有一组数据:2、4、4、5、8,这组数据的众数是( )A、2 B、4 C、5 D、83. 若代数式 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、4. 据央视网消息,全国广大共产党员积极响应党中央号召,踊跃捐款,表达对新冠肺炎疫情防控工作的支持.据统计,截至2020年3月10日,全国已有7436万多名党员自愿捐款,共捐款76.8亿元.76.8亿用科学记数法可表示为( )A、 B、 C、 D、5. 如图, 中, , ,则 的值为( )
 A、 B、 C、 D、6. 如图, 中, , ,顶点C在直线b上,若a∥b, ,则 的度数为( )
A、 B、 C、 D、6. 如图, 中, , ,顶点C在直线b上,若a∥b, ,则 的度数为( )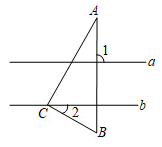 A、 B、 C、 D、7. 如图,扇形 中, ,以 为直径作半圆,若 ,则阴影部分的周长为( )
A、 B、 C、 D、7. 如图,扇形 中, ,以 为直径作半圆,若 ,则阴影部分的周长为( )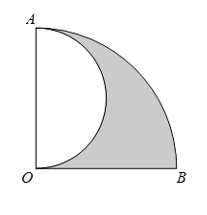 A、 B、 C、 D、8. 若一次函数 的图像经过点 ,则不等式 的解集为( )A、 B、 C、 D、9. 宽和长的比为 的矩形称为黄金矩形,如图,黄金矩形 中,宽 ,将黄金矩形 沿 折叠,使得点C落在点A处,点D落在点 处,则 的面积为( )
A、 B、 C、 D、8. 若一次函数 的图像经过点 ,则不等式 的解集为( )A、 B、 C、 D、9. 宽和长的比为 的矩形称为黄金矩形,如图,黄金矩形 中,宽 ,将黄金矩形 沿 折叠,使得点C落在点A处,点D落在点 处,则 的面积为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点C从点A出发以2个单位长度 的速度沿线段 向点O匀速移动,同时点D从点O出发以1个单位长度 的速度沿线段 向点B匀速移动,点P为线段 的中点,在点C从点A移动到点O的过程中,点P移动的路径长为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点C从点A出发以2个单位长度 的速度沿线段 向点O匀速移动,同时点D从点O出发以1个单位长度 的速度沿线段 向点B匀速移动,点P为线段 的中点,在点C从点A移动到点O的过程中,点P移动的路径长为( ) A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题
-
11. 计算: .12. 分解因式: .13. 若 ,则 .14. 二次函数 的顶点坐标为.15. 转动如图所示的转盘一次,指针指向阴影部分的概率为.
 16. 如图, 内接于 ,C为弧 的中点,若 ,则 .
16. 如图, 内接于 ,C为弧 的中点,若 ,则 .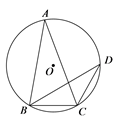 17. 如图, 中, , , ,射线 与边 交于点D,E、F分别为 、 中点,设点E、F到射线 的距离分别为m、n,则 的最大值为.
17. 如图, 中, , , ,射线 与边 交于点D,E、F分别为 、 中点,设点E、F到射线 的距离分别为m、n,则 的最大值为.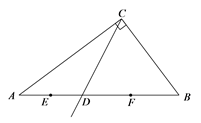 18. 如图,折线 中, , ,将折线 绕点A按逆时针方向旋转,得到折线 ,点B的对应点落在线段 上的点D处,点C的对应点落在点E处,连接 ,若 ,则 °.
18. 如图,折线 中, , ,将折线 绕点A按逆时针方向旋转,得到折线 ,点B的对应点落在线段 上的点D处,点C的对应点落在点E处,连接 ,若 ,则 °.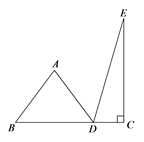
三、解答题
-
19. 计算: .20. 解不等式 ,并把它的解集在数轴上表示出来.
 21. 先化简,再求值: ,其中 .22. 如图, 中,D、E分别为边 、 中点,连接 并延长至点F,使得 ,连接 .
21. 先化简,再求值: ,其中 .22. 如图, 中,D、E分别为边 、 中点,连接 并延长至点F,使得 ,连接 .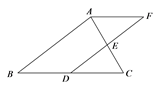 (1)、求证: ;(2)、若 , ,求四边形 的周长.23. 新学期复学后,学校为了保障学生的出行安全,随机调查了部分学生的上学方式(每位学生从乘私家车、坐公交、骑车和步行4种方式中限选1项),根据调查数据制作了如图所示的不完整的统计表和扇形统计图.
(1)、求证: ;(2)、若 , ,求四边形 的周长.23. 新学期复学后,学校为了保障学生的出行安全,随机调查了部分学生的上学方式(每位学生从乘私家车、坐公交、骑车和步行4种方式中限选1项),根据调查数据制作了如图所示的不完整的统计表和扇形统计图. (1)、本次学校共调查了名学生, , ;(2)、求扇形统计图中“步行”对应扇形的圆心角;(3)、甲、乙两位同学住在同一小区,且都坐公交车上学,有 、 、 三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.24. 新冠肺炎疫情期间,佩戴口罩是做好个人防护的重要举措.小明家先后两次在同一电商平台以相同的单价免邮购买了A、B两种型号的口罩.第一次购买20个A型口罩,30个B型口罩,共花费190元;第二次购买30个A型口罩,20个B型口罩,共花费160元.(1)、求A、B两种型号口罩的单价;(2)、“五一”期间,该电商平台举行促销活动,小明发现同样花费160元购买B型口罩,以活动价购买可以比原价多买8个,求“五一”期间B型口罩的活动价.25. 如图, 中,顶点A、B在反比例函数 的图像上,顶点C在x轴的正半轴上, .
(1)、本次学校共调查了名学生, , ;(2)、求扇形统计图中“步行”对应扇形的圆心角;(3)、甲、乙两位同学住在同一小区,且都坐公交车上学,有 、 、 三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.24. 新冠肺炎疫情期间,佩戴口罩是做好个人防护的重要举措.小明家先后两次在同一电商平台以相同的单价免邮购买了A、B两种型号的口罩.第一次购买20个A型口罩,30个B型口罩,共花费190元;第二次购买30个A型口罩,20个B型口罩,共花费160元.(1)、求A、B两种型号口罩的单价;(2)、“五一”期间,该电商平台举行促销活动,小明发现同样花费160元购买B型口罩,以活动价购买可以比原价多买8个,求“五一”期间B型口罩的活动价.25. 如图, 中,顶点A、B在反比例函数 的图像上,顶点C在x轴的正半轴上, . (1)、若 ,求k的值;(2)、若 , , ,求点C的坐标.26. 如图, 为 的直径, 为 的切线, ,交 于点D,E为弧 的中点,连接 ,交 于点F.
(1)、若 ,求k的值;(2)、若 , , ,求点C的坐标.26. 如图, 为 的直径, 为 的切线, ,交 于点D,E为弧 的中点,连接 ,交 于点F. (1)、求证: 为 的切线;(2)、求证: ;(3)、若 ,求 .27. 如图①, 中, , .动点 在 的边上按 的路线匀速移动,当点 到达 点时停止移动;动点Q以 的速度在 的边上按 的路线匀速移动,当点Q到达C点时停止移动.已知点 、点Q同时开始移动,同时停止移动(即同时到达各自的终止位置).设动点 移动的时间为 , 的面积为 ,S与t的函数关系如图②所示.
(1)、求证: 为 的切线;(2)、求证: ;(3)、若 ,求 .27. 如图①, 中, , .动点 在 的边上按 的路线匀速移动,当点 到达 点时停止移动;动点Q以 的速度在 的边上按 的路线匀速移动,当点Q到达C点时停止移动.已知点 、点Q同时开始移动,同时停止移动(即同时到达各自的终止位置).设动点 移动的时间为 , 的面积为 ,S与t的函数关系如图②所示. (1)、图①中 ,图②中 ;(2)、求S与t的函数表达式;(3)、当 为何值时, 为等腰三角形.28. 如图,二次函数 (其中 )的图像与x轴交于A、B两点,与y轴交于点C.
(1)、图①中 ,图②中 ;(2)、求S与t的函数表达式;(3)、当 为何值时, 为等腰三角形.28. 如图,二次函数 (其中 )的图像与x轴交于A、B两点,与y轴交于点C. (1)、点a的坐标为 , ;(2)、若D为 的外心,且 与 的面积之比为 ,求m的值;(3)、在(2)的条件下,试探究抛物线 上是否存在点E,使得 ,若存在,求出点 的坐标;若不存在,请说明理由.
(1)、点a的坐标为 , ;(2)、若D为 的外心,且 与 的面积之比为 ,求m的值;(3)、在(2)的条件下,试探究抛物线 上是否存在点E,使得 ,若存在,求出点 的坐标;若不存在,请说明理由.