江苏省苏州市2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 下列运算正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、(-2a2)3=-8a6 D、a8÷a4=a23. 随着高铁的发展,预计2020年济南西客站客流量将达到2150万人,数字2150用科学记数法表示为( )A、0.215×104 B、2.15×103 C、2.15×104 D、21.5×1024. 下列说法中正确的是( )A、掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 B、“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件 C、“同位角相等”这一事件是不可能事件 D、“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件5. 设点A(x1 , y1)和点B(x2 , y2)是反比例函数y= 图象上的两点,当x1<x2<0时,y1>y2 , 则一次函数y=-2x+k的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图是某几何体的三视图及相关数据,则该几何体的侧面积是( )
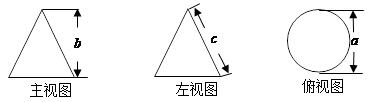 A、 B、 C、 D、7.
A、 B、 C、 D、7.如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )
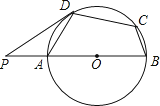 A、40° B、35° C、30° D、45°8. 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A、40° B、35° C、30° D、45°8. 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( ) A、20海里 B、40海里 C、海里 D、海里9. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE 沿AE折叠,点B落在点F处,连接FC,则tan∠ECF = ( )
A、20海里 B、40海里 C、海里 D、海里9. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE 沿AE折叠,点B落在点F处,连接FC,则tan∠ECF = ( ) A、
A、 B、
B、 C、
C、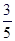 D、
D、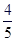 10. 在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A、B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM的延长线与x轴交于点N(n,0),如图3,当m= 时,n的值为( )
10. 在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A、B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM的延长线与x轴交于点N(n,0),如图3,当m= 时,n的值为( )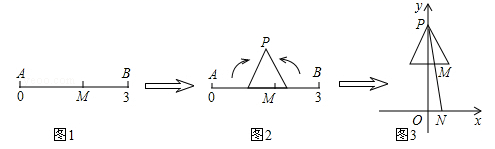 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数 中,自变量x的取值范围是.12. 分解因式:a3﹣2a2+a= .13. 已知 , 是二元一次方程组 的解,则代数式 的值为.14. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .15. 如图,在△ABC中,BC=6,以点A为圆心,2为半径的☉A与BC相切于点D,交AB于点E,交AC于点F,点P是优弧 上的一点,且∠EPF=50°,则图中阴影部分的面积是.
 16. 把二次函数y=x2+bx+c的图象向下平移1个单位长度,再向左平移2个单位长度后,得到的抛物线的顶点坐标为(﹣1,0),则b+c的值为 .17. 如图,已知点A、B在双曲线y= (x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,若△ABP的面积为3,则k=.
16. 把二次函数y=x2+bx+c的图象向下平移1个单位长度,再向左平移2个单位长度后,得到的抛物线的顶点坐标为(﹣1,0),则b+c的值为 .17. 如图,已知点A、B在双曲线y= (x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,若△ABP的面积为3,则k=. 18. 如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是 上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为.
18. 如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是 上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为.
三、解答题
-
19. 计算:(-3)2- +|-2|20. 先化简,再求值: ,其中,a= +1.21. 解不等式组22. 在端午节来临之际,某商店订购了A型和B型两种粽子.A型粽子28元/千克,B型粽子24元/千克.若B型粽子的数量比A型粽子的2倍少20千克,购进两种粽子共用了2560元,求两种型号粽子各多少千克.
23. 已知锐角△ABC,∠ABC=45°,AD⊥BC于D,BE⊥AC于E,交AD于F.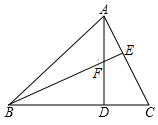 (1)、求证:△BDF≌△ADC;(2)、若BD=4,DC=3,求线段BE的长度.24. 某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级(2)班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
(1)、求证:△BDF≌△ADC;(2)、若BD=4,DC=3,求线段BE的长度.24. 某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级(2)班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:八年级(2)班参加球类活动人数情况统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
八年级(2)班学生参加球类活动人数情况扇形统计图
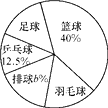
根据图中提供的信息,解答下列问题:
(1)、a= , b= .(2)、该校八年级学生共有600人,则该年级参加足球活动的人数约人;
(3)、该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
25. 如图,点A、B分别在y轴和x轴上,BC⊥AB(点C和点O在直线AB的两侧),点C的坐标为(4,n)过点C的反比例函数y= (x>0)的图象交边AC于点D(n+ ,3). (1)、求反比例函数的表达式;(2)、求点B的坐标.26. 如图,钝角△ABC中,AB=AC,BC=2 ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)、求反比例函数的表达式;(2)、求点B的坐标.26. 如图,钝角△ABC中,AB=AC,BC=2 ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F. (1)、求证:EF⊥AC.(2)、连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.27. 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点 Q,PM∥OB交OA于点M.
(1)、求证:EF⊥AC.(2)、连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.27. 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点 Q,PM∥OB交OA于点M. (1)、若∠AOB=45°,OM=4,OQ= ,求证:CN⊥OB;(2)、当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
(1)、若∠AOB=45°,OM=4,OQ= ,求证:CN⊥OB;(2)、当点N在边OB上运动时,四边形OMPQ始终保持为菱形.①问: 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求 的取值范围.
28. 如图1,抛物线 与 轴交于点 ,与y轴交于点 ,在 轴上有一动点 ,过点E作x轴的垂线交直线 于点N,交抛物线于点P,过点P作 于点M.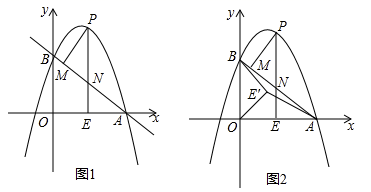 (1)、求a的值和直线 的函数表达式;(2)、设 的周长为 , 的周长为 ,若 ,求m的值;(3)、如图2,在(2)条件下,将线段 绕点O逆时针旋转得到 ,旋转角为 ,连接 、 ,求 的最小值.
(1)、求a的值和直线 的函数表达式;(2)、设 的周长为 , 的周长为 ,若 ,求m的值;(3)、如图2,在(2)条件下,将线段 绕点O逆时针旋转得到 ,旋转角为 ,连接 、 ,求 的最小值.