江苏省连云港市连云区2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列计算中,正确的是( )A、a3+a2=a5 B、a3·a2=a5 C、(a3)2=a5 D、a3-a2=a3. 如图所示的几何体的俯视图应该是( )
 A、
A、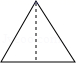 B、
B、 C、
C、 D、
D、 4. 九(1)班同学采用“小组合作学习”的方式进行学习,值周班长每周对各小组合作学习情况进行综合评分,下表是其中一周的评分结果:
4. 九(1)班同学采用“小组合作学习”的方式进行学习,值周班长每周对各小组合作学习情况进行综合评分,下表是其中一周的评分结果:组别
一
二
三
四
五
六
七
分值
90
96
59
90
91
85
90
这组数据中的中位数和众数分别是( )
A、89,90 B、90,90 C、88,95 D、90,955. 在反比例函数y= 图像的每一支上,y都随x的增大而增大,则k的取值范围是( )A、k>1 B、k>0 C、k≥1 D、k<16. 如图,AB是☉O的直径,点C在AB的延长线上,CD切☉O于点D,若∠A=25°,则∠C的度数是( )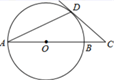 A、40º B、50º C、55º D、65º7. 竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ ,若小球经过 秒落地,则小球在上抛过程中,第( )秒离地面最高.A、 B、 C、 D、8. 如图,在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点,若DE平分△ABC的周长,则DE的长是( )
A、40º B、50º C、55º D、65º7. 竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ ,若小球经过 秒落地,则小球在上抛过程中,第( )秒离地面最高.A、 B、 C、 D、8. 如图,在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点,若DE平分△ABC的周长,则DE的长是( )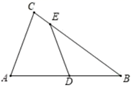 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
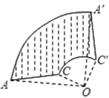
9. 若分式 有意义,则x的取值范围是.10. 分解因式:3a2+6ab+3b2=.11. 五一假期,连云港市接待旅游总人数1760000人次,将1760000用科学记数法表示.12. 一个长、宽分别为m、n的长方形的周长为14,面积为8,则m2n+mn2的值为 .13. 关于x的方程x2+x-2a=0有实数根,则实数a的取值范围是.14. 如图,AC是汽车挡风玻璃的挂雨刷,如果AO=65cm,CO=15cm,则AC绕点O旋转90°时,则挂雨刷AC扫过的面积为cm².
 15. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是
15. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是 16. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以A为圆心4为半径D圆上的一点,连接BD,点M为BD中点,线段CM长度的最小值是.
16. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以A为圆心4为半径D圆上的一点,连接BD,点M为BD中点,线段CM长度的最小值是.
三、解答题
-
17. 计算:( )-1- +(-2)218. 计算(1- )÷19. 解不等式组:20. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
组别
A
B
C
D
E
分组(元)
0≤x<30
30≤x<60
60≤x<90
90≤x<120
120≤x<150
频数
4
a
20
8
2
请根据以上图标,解答下列问题:
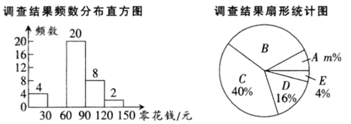 (1)、填空:这次调查的样本容量是 , a= , m=;(2)、补全频数分布直方图;(3)、求扇形统计图中扇形B的圆心角度数;(4)、该校共有1000人,请估计每月零花钱的数额x在30≤x<90范围的人数;21. 某中学为迎接国庆七十周年,矩形了“祖国在我心中”演讲比赛,经预赛,七、八年级各有一名同学进入决赛,九年级有2名同学进入决赛:(1)、九年级同学获得第一名的概率;(2)、求九年级同学获得前两名的概率.22. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
(1)、填空:这次调查的样本容量是 , a= , m=;(2)、补全频数分布直方图;(3)、求扇形统计图中扇形B的圆心角度数;(4)、该校共有1000人,请估计每月零花钱的数额x在30≤x<90范围的人数;21. 某中学为迎接国庆七十周年,矩形了“祖国在我心中”演讲比赛,经预赛,七、八年级各有一名同学进入决赛,九年级有2名同学进入决赛:(1)、九年级同学获得第一名的概率;(2)、求九年级同学获得前两名的概率.22. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,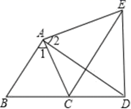 (1)、试说明△ABD与△ACE全等的理由;(2)、如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.23. 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们的东北方向距离12海里处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻艇以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻队出发到成功拦截捕鱼船所用的时间.
(1)、试说明△ABD与△ACE全等的理由;(2)、如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.23. 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们的东北方向距离12海里处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻艇以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻队出发到成功拦截捕鱼船所用的时间. 24. 如图1,直线y=x-1交x轴、y轴于A、B点,点P(1, ,且S四边形PAOB=3.5,双曲线y= 经过点P.
24. 如图1,直线y=x-1交x轴、y轴于A、B点,点P(1, ,且S四边形PAOB=3.5,双曲线y= 经过点P.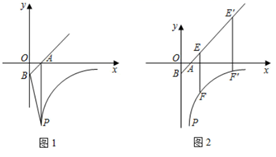 (1)、求k的值;(2)、如图2,直线 )交射线BA于E,交双曲线y= 于F,将直线 向右平移4个单位长度后交射线于 ,交双曲线y= 于 ,若 ,求 的值.25. 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为 米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设 的长度为 米,矩形区域 的面积为 米 .
(1)、求k的值;(2)、如图2,直线 )交射线BA于E,交双曲线y= 于F,将直线 向右平移4个单位长度后交射线于 ,交双曲线y= 于 ,若 ,求 的值.25. 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为 米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设 的长度为 米,矩形区域 的面积为 米 . (1)、求证: ;(2)、求y与x之间的函数关系式,并写出自变量x的取值范围;(3)、x为何值时,y有最大值?最大值是多少?26. 如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)、求证: ;(2)、求y与x之间的函数关系式,并写出自变量x的取值范围;(3)、x为何值时,y有最大值?最大值是多少?26. 如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.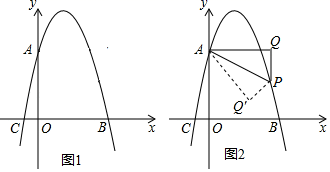 (1)、求抛物线的函数表达式和点C的坐标;(2)、若△AQP∽△AOC,求点P的横坐标;(3)、如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.27. 爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)、求抛物线的函数表达式和点C的坐标;(2)、若△AQP∽△AOC,求点P的横坐标;(3)、如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.27. 爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c. (1)、(特例研究)
(1)、(特例研究)如图1,当tan∠PAB=1,c=4 时,a=b=;
(2)、(归纳证明)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图2证明你的结论;
(3)、(拓展证明)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF交BE相较于点G,AD=3 ,AB=3,求AF的长.