湖北省黄石市阳新县2020年数学中考三模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. -1 的倒数是( )A、- B、- C、-1 D、-2. 下列既是中心对称又是轴对称图形的( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,下列关于物体的主视图画法正确的是( )
3. 如图,下列关于物体的主视图画法正确的是( )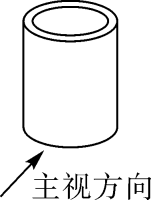 A、
A、 B、
B、 C、
C、 D、
D、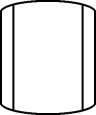 4. 下列运算正确的是( )A、 B、 C、 D、5. 函数 的自变量x的取值范围是( )A、 B、 C、 D、 且6. 不等式组 有3个整数解,则 的取值范围是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 函数 的自变量x的取值范围是( )A、 B、 C、 D、 且6. 不等式组 有3个整数解,则 的取值范围是( )
A、 B、 C、 D、7. 已知点 向右平移3个单位,之后又向下移7个单位,得到点N、若点N恰好第三象限的角平分线上,则 的值为( )A、2 B、0 C、3 D、8. 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )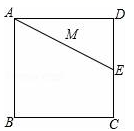 A、 cm或 cm B、 cm C、 cm或 cm D、 cm或 cm9. 在⊙O中,AB为直径,点C为圆上一点,将劣弧 沿弦AC翻折交AB于点D , 连结CD . 如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
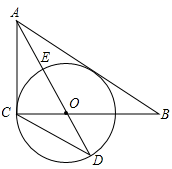
A、 cm或 cm B、 cm C、 cm或 cm D、 cm或 cm9. 在⊙O中,AB为直径,点C为圆上一点,将劣弧 沿弦AC翻折交AB于点D , 连结CD . 如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( ) A、35° B、40° C、45° D、65°10. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1
A、35° B、40° C、45° D、65°10. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1二、填空题
-
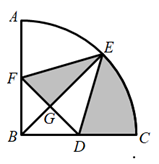
11. 分解因式: .12. “白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084可以用科学记数法表示为.13. 一个样本为1,3,2,2,a,b,c,已知这个样本的众数为3,平均数为2,则这组数据的中位数为 .14. 如图,在圆心角为 的扇形 中,半径 ,点E为 的中点,点 分别是边 的中点,连接 ,连接 交 于点G,则图中阴影部分的面积为.
 15. 如图, 是等腰直角三角形, ,点 分别是边 与 的中点, 是 上一点,以 为一直角边作等腰直角 ,且 ,若 ,则 .
15. 如图, 是等腰直角三角形, ,点 分别是边 与 的中点, 是 上一点,以 为一直角边作等腰直角 ,且 ,若 ,则 .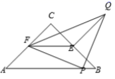
三、解答题
-
16. 计算:17. 先化简 ,再从-2,-1,0,1,2中选取一个合适的数作为x的值代入求值.18. 刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高 米. 米,当吊臂顶端由A点抬升至 点(吊臂长度不变时),地面 处的重物(大小忽略不计)被吊至 处,紧绷着的吊缆 .且 .
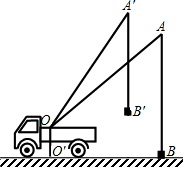 (1)、求此重物在水平方向移动的距离及在竖直方向移动的距离;(2)、若这台吊车工作时吊杆最大水平旋转角度为 ,吊杆与水平线的倾角可以从 转到 ,求吊车工作时,工作人员不能站立的区域的面积.19. 如图, 和 中, , , ,AB,DE相交于点F,AD,BC相交于点G.
(1)、求此重物在水平方向移动的距离及在竖直方向移动的距离;(2)、若这台吊车工作时吊杆最大水平旋转角度为 ,吊杆与水平线的倾角可以从 转到 ,求吊车工作时,工作人员不能站立的区域的面积.19. 如图, 和 中, , , ,AB,DE相交于点F,AD,BC相交于点G.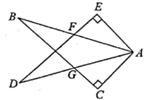 (1)、求证: ;(2)、若 , ,求DG的长.20. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
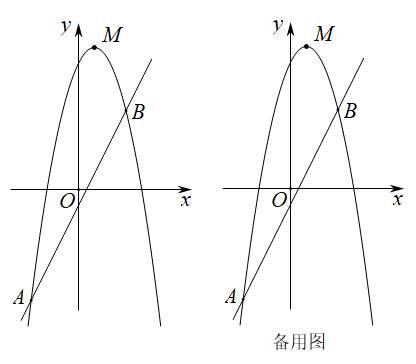
(1)、求证: ;(2)、若 , ,求DG的长.20. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.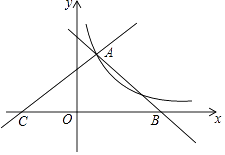 (1)、求y与x之间的函数关系式;
(1)、求y与x之间的函数关系式;
(2)、直接写出当x>0时,不等式 x+b> 的解集;(3)、若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.21. 已知关于x的方程ax2+(3﹣2a)x+a﹣3=0.(1)、求证:无论a为何实数,方程总有实数根.(2)、如果方程有两个实数根x1 , x2 , 当|x1﹣x2|= 时,求出a的值.22. 如图,有四张背面完全相同的纸牌 ,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀. (1)、从中随机摸出一张,求摸出的牌正面图形是中心对称图形的概率;(2)、小明和小亮约定做一个游戏,其规则如下:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌正面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表或画树状图的方法说明. (纸牌用 表示)23. 某商店销售A型和B型两种学习机,其中用10000元采购A型学习机台数和用8000元采购 型学习机台数相等,且一台A型学习机比一台B型学习机进价多100元.(1)、求一台A型和B型学习机价格各是多少元?(2)、若购进 型学习机共100台,其中B型的进货量不超过A型的2倍,设购进A型学习机x台.
(1)、从中随机摸出一张,求摸出的牌正面图形是中心对称图形的概率;(2)、小明和小亮约定做一个游戏,其规则如下:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌正面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表或画树状图的方法说明. (纸牌用 表示)23. 某商店销售A型和B型两种学习机,其中用10000元采购A型学习机台数和用8000元采购 型学习机台数相等,且一台A型学习机比一台B型学习机进价多100元.(1)、求一台A型和B型学习机价格各是多少元?(2)、若购进 型学习机共100台,其中B型的进货量不超过A型的2倍,设购进A型学习机x台.①求x的取值范围.
②已知 型学习机售价均是900元/台,实际进货时,厂家对A型学习机在原进货价的基础,上下调 元,且限定商店最多购进A型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润W(元)的最大值.