贵州省遵义市红花岗区2020年数学中考二模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 下列各数属于无理数的是( )A、 B、 C、0 D、12. 国家发改委2月7日紧急下达第二批中央预算内投资2亿元人民币,专项补助湖北多家医院的重症治疗病区建设,其中数据2亿元用科学记数法表示为( )A、2×107元 B、2×108元 C、2×109元 D、0.2×109元3. 下列运算正确的是( )A、2a3+3a2=5a5 B、(﹣a)2+a2=0 C、(a﹣b)2=a2﹣b2 D、3a3b2÷a2b=3ab4. 已知x1、x2是关于x的方程x2+mx﹣1=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2<0 C、x1•x2>0 D、x1>0,x2<05. 为全力抗击“新冠肺炎“疫情,响应政府“停课不停学”号召,遵义市教育局发布关于疫情防控期间开展在线教育教学的通知:从2月10日开始,全市九年级按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2月10日在线答疑问题总个数如表所示:
学科
语文
数学
英语
物理
化学
道法
历史
数量/个
26
28
28
26
24
21
22
则2月10日该中学九年级七科老师在线答疑问题总个数的平均数是( )
A、22 B、24 C、25 D、266. 如图是由7个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的左视图是( ) A、
A、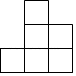 B、
B、 C、
C、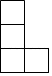 D、
D、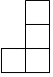 7. 如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
7. 如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( ) A、(m﹣n)2=m2﹣2mn+n2 B、(m+n)2=m2+2mn+n2 C、(m﹣n)2=m2+n2 D、m2﹣n2=(m+n)(m﹣n)8. 如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=36°,则∠B等于( )。
A、(m﹣n)2=m2﹣2mn+n2 B、(m+n)2=m2+2mn+n2 C、(m﹣n)2=m2+n2 D、m2﹣n2=(m+n)(m﹣n)8. 如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=36°,则∠B等于( )。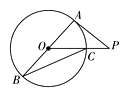 A、27° B、32° C、36° D、54°9. 如图点A为反比例函数y= (k≠0)图形上的一点,过点A作AB⊥y轴于B,点C为x轴上的一个动点,△ABC的面积为3,则k的值为( )
A、27° B、32° C、36° D、54°9. 如图点A为反比例函数y= (k≠0)图形上的一点,过点A作AB⊥y轴于B,点C为x轴上的一个动点,△ABC的面积为3,则k的值为( ) A、3 B、6 C、9 D、1210. 把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P , 则∠APG=( )
A、3 B、6 C、9 D、1210. 把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P , 则∠APG=( )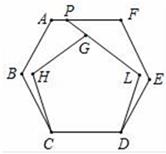 A、141° B、144° C、147° D、150°11. 如图,已知l1∥l2∥l3 , 相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sina的值是( )
A、141° B、144° C、147° D、150°11. 如图,已知l1∥l2∥l3 , 相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sina的值是( )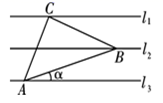 A、 B、 C、 D、12. 如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:①抛物线的对称轴是直线x=1;②若OC=OB,则c=2;③若M(x0 , y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;④抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2.其中真命题个数是( )
A、 B、 C、 D、12. 如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:①抛物线的对称轴是直线x=1;②若OC=OB,则c=2;③若M(x0 , y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;④抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2.其中真命题个数是( )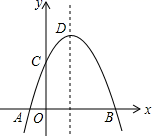 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
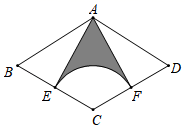
13. 在函数y= 中,自变量x的取值范围是 .14. 计算: =。15. 如图,在菱形ABCD中,点E是BC的中点,以C为圆心,CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60°,则阴影部分的面积为.
 16. 如图是一张矩形纸片ABCD,已知AB=8,AD=6,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在矩形ABCD的某一条边上,则等腰三角形AEP的底边上的高的长是.
16. 如图是一张矩形纸片ABCD,已知AB=8,AD=6,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在矩形ABCD的某一条边上,则等腰三角形AEP的底边上的高的长是.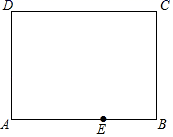
三、解答题
-
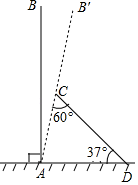
17.(1)、计算:﹣12008+3tan60°﹣|3﹣ |;(2)、已知关于x的方程2x2+3x﹣m=0没有实数根,求m的取值范围.18. 先化简,再求值:( +a+2) ,其中a为不等式组 的整数解.19. 某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
 20. 四边形ABCD是正方形,PA是过正方形顶点A的直线,作DE⊥PA于E,将射线DE绕点D逆时针旋转45°与直线PA交于点F.
20. 四边形ABCD是正方形,PA是过正方形顶点A的直线,作DE⊥PA于E,将射线DE绕点D逆时针旋转45°与直线PA交于点F.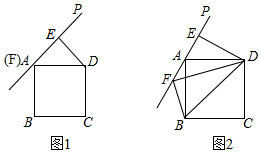 (1)、如图1,当∠PAD=45°时,点F恰好与点A重合,则 的值为;(2)、如图2,若45°<∠PAD<90°,连接BF、BD,试求 的值,并说明理由.21. 某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与《新型冠状病毒防治与预防知识》作答(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行数据统计、数据分析.
(1)、如图1,当∠PAD=45°时,点F恰好与点A重合,则 的值为;(2)、如图2,若45°<∠PAD<90°,连接BF、BD,试求 的值,并说明理由.21. 某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与《新型冠状病毒防治与预防知识》作答(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行数据统计、数据分析.甲
85
80
95
85
90
95
100
65
75
85
90
90
70
100
90
80
80
90
98
75
乙
80
60
80
85
95
65
90
85
100
80
95
75
80
80
70
100
95
75
90
90
表1分数统计表
成绩
小区
60≤x≤70
70<x≤80
80<x≤90
90<x≤100
甲
2
5
a
b
乙
3
7
5
5
表2:频数分布表
统计量
小区
平均数
中位数
众数
甲
85.75
87.5
c
乙
83.5
d
80
表3:统计量
(1)、填空:a= , b= , c= , d=;(2)、甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;(3)、对于此次抽样调查中测试成绩为60≤x≤70的居民,社区鼓励他们重新学习,然后从中随机抽取两名居民进行测试,求刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.22. 某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.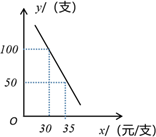 (1)、求y与x之间的函数关系式.(2)、由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?23. 如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
(1)、求y与x之间的函数关系式.(2)、由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?23. 如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.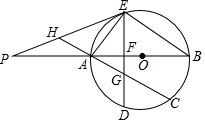 (1)、求证:PE是⊙O的切线;(2)、连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;(3)、若tan∠P= ,试求 的值.24. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).
(1)、求证:PE是⊙O的切线;(2)、连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;(3)、若tan∠P= ,试求 的值.24. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).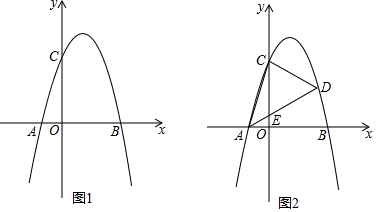 (1)、求抛物线的解析式;(2)、如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);(3)、在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);(3)、在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.