广西梧州市2020年数学中考一模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 若 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、4. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 已知 ,则 的补角是( )A、 B、 C、 D、6. 在平面直角坐标系中,点A(3,-2)关于x轴对称的点是 ,则 的坐标是( )A、 B、 C、 D、7. 已知 ,则下列式子中,正确的是( )A、 B、 C、 D、8. 在西江上,一艘江轮航行在相距76km的两地港口,顺流而行需4h,逆流而行需4.7h,设江轮在静水中的速度为xkm/h,水流速度是ykm/h,则下面所列的方程组中,正确的是( )A、 B、 C、 D、9. 如图,在菱形 中,对角线 、 交于点O,点 是 的中点,连结 , , ,则 的周长是( )
5. 已知 ,则 的补角是( )A、 B、 C、 D、6. 在平面直角坐标系中,点A(3,-2)关于x轴对称的点是 ,则 的坐标是( )A、 B、 C、 D、7. 已知 ,则下列式子中,正确的是( )A、 B、 C、 D、8. 在西江上,一艘江轮航行在相距76km的两地港口,顺流而行需4h,逆流而行需4.7h,设江轮在静水中的速度为xkm/h,水流速度是ykm/h,则下面所列的方程组中,正确的是( )A、 B、 C、 D、9. 如图,在菱形 中,对角线 、 交于点O,点 是 的中点,连结 , , ,则 的周长是( ) A、14 B、13 C、9 D、810. 小芳给校方提供学生体育锻炼的情况报告,在校内对全校学生进行了抽样调查,每位学生只选择一项自己最喜欢的体育运动.其中,a代表最喜欢参加兵乒球运动;b代表最喜欢参加羽毛球运动;c代表最喜欢气排球运动;d代表最喜欢篮球运动,下图是她还未完成的条形统计图与扇形统计图,根据统计图所给出的信息,这个样本中最喜欢篮球运动(即d)的百分率与人数是( )
A、14 B、13 C、9 D、810. 小芳给校方提供学生体育锻炼的情况报告,在校内对全校学生进行了抽样调查,每位学生只选择一项自己最喜欢的体育运动.其中,a代表最喜欢参加兵乒球运动;b代表最喜欢参加羽毛球运动;c代表最喜欢气排球运动;d代表最喜欢篮球运动,下图是她还未完成的条形统计图与扇形统计图,根据统计图所给出的信息,这个样本中最喜欢篮球运动(即d)的百分率与人数是( )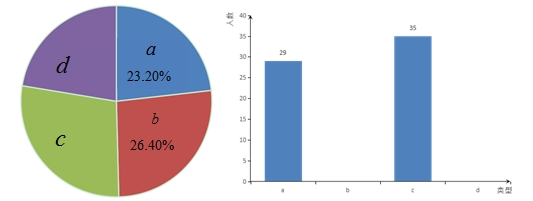 A、24,26% B、33,26.4% C、28,22.4% D、25,23.6%11. 如图,在ΔABC中,∠1=∠C,AB=8,BD=4,则DC=( )
A、24,26% B、33,26.4% C、28,22.4% D、25,23.6%11. 如图,在ΔABC中,∠1=∠C,AB=8,BD=4,则DC=( )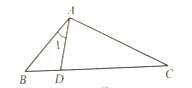 A、8 B、10 C、12 D、1612. 在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点(1,2),(5,3),则下列说法正确的是( )
A、8 B、10 C、12 D、1612. 在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点(1,2),(5,3),则下列说法正确的是( )①抛物线与y轴有交点②若抛物线经过点(2,2),则抛物线的开口向上③抛物线的对称轴不可能是x=3④若抛物线的对称轴是x=4,则抛物线与x轴有交点
A、①②③④ B、①②③ C、①③④ D、②④二、填空题
-
13. 计算: =; =; = .14. 计算: .15. 解方程: 的解是 .16. 如图, 是圆⊙O的直径,点D、C为⊙O上的点, ,则 度.
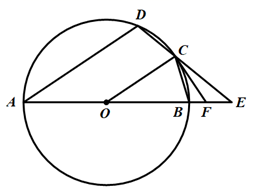
 17. 如图, 为等边三角形,延长 到点D,且 ,连结 ,作 交 于点E,若 ,则 cm.
17. 如图, 为等边三角形,延长 到点D,且 ,连结 ,作 交 于点E,若 ,则 cm.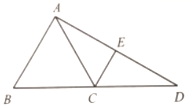 18. 如图,在圆上放置一些围棋子,图①中,有3个围棋子,图②中有8个围棋子,图③中有15个围棋子,按此规律,图⑧中有80个围棋子,那么图⑩中有个围棋子.
18. 如图,在圆上放置一些围棋子,图①中,有3个围棋子,图②中有8个围棋子,图③中有15个围棋子,按此规律,图⑧中有80个围棋子,那么图⑩中有个围棋子.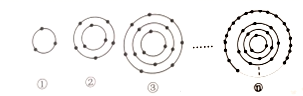
三、解答题
-
19. 计算: .20. 解方程: .21. 如图,在平行四边形ABCD中, 于点E, 于点F.求证: .
 22. 某单位共有280位员工参加了社会公益捐款活动,从中任意抽取了12位员工的捐款数额,记录如下:
22. 某单位共有280位员工参加了社会公益捐款活动,从中任意抽取了12位员工的捐款数额,记录如下:捐款数额/元
30
50
80
100
员工人数
2
5
3
2
估计该单位的捐款总额.
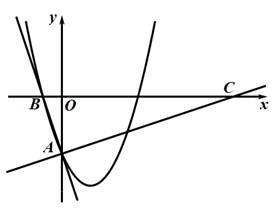
23. 如图,在平面直角坐标系中,直线 与双曲线 分别交于点A、B两点,过A点作x轴的垂线AC,垂足为点C,OC=1, .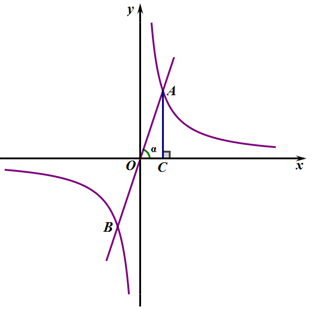 (1)、分别求出 的值;(2)、当 时,求x的取值范围.24. 在完善基础设施、改善市容市貌、提升城市品质过程中,2019年我市开展人行道改造工程,需要花岗岩地板砖铺设人行道.现租用甲、乙两种货车运载地板砖,已知一辆甲车每次运载的重量比一辆乙车多2吨,且甲车运载16吨地板砖和乙车运载12吨地板砖所用的车辆数相同.(1)、甲、乙两种货车每次运载地板砖各多少吨?(2)、现租用甲车a辆、乙车b辆,刚好运载地板砖100吨,且a≤3b,共有多少种租车方案?(3)、在(2)中已知一辆甲车每次的运费是380元,一辆乙车每次的运费是300元,如何租用甲、乙两种车可使得总运费最低?求出最低总运费.
(1)、分别求出 的值;(2)、当 时,求x的取值范围.24. 在完善基础设施、改善市容市貌、提升城市品质过程中,2019年我市开展人行道改造工程,需要花岗岩地板砖铺设人行道.现租用甲、乙两种货车运载地板砖,已知一辆甲车每次运载的重量比一辆乙车多2吨,且甲车运载16吨地板砖和乙车运载12吨地板砖所用的车辆数相同.(1)、甲、乙两种货车每次运载地板砖各多少吨?(2)、现租用甲车a辆、乙车b辆,刚好运载地板砖100吨,且a≤3b,共有多少种租车方案?(3)、在(2)中已知一辆甲车每次的运费是380元,一辆乙车每次的运费是300元,如何租用甲、乙两种车可使得总运费最低?求出最低总运费.