广西防城港市2020年数学中考全真模拟试卷(一)
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 下面的数中,与﹣3的和为0的是 ( )A、3 B、﹣3 C、 D、-2. 下列计算正确的是( )A、a2•a4=a8 B、 =±2 C、 =﹣1 D、a4÷a2=a23. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列叙述正确的是( )A、方差越大,说明数据就越稳定 B、在不等式两边同乘或同除以一个不为0的数时,不等号的方向不变 C、不在同一直线上的三点确定一个圆 D、两边及其一边的对角对应相等的两个三角形全等5. 函数 的自变量x的取值范围是( )A、x≤2 B、x≥2且x≠3 C、x≥2 D、x≤2且x≠36. 若 与 是同类项,则 的值为( )A、1 B、2 C、3 D、47. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
4. 下列叙述正确的是( )A、方差越大,说明数据就越稳定 B、在不等式两边同乘或同除以一个不为0的数时,不等号的方向不变 C、不在同一直线上的三点确定一个圆 D、两边及其一边的对角对应相等的两个三角形全等5. 函数 的自变量x的取值范围是( )A、x≤2 B、x≥2且x≠3 C、x≥2 D、x≤2且x≠36. 若 与 是同类项,则 的值为( )A、1 B、2 C、3 D、47. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )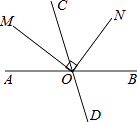 A、35° B、45° C、55° D、65°8. AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )
A、35° B、45° C、55° D、65°8. AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( ) A、15° B、30° C、40° D、45°9. 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
A、15° B、30° C、40° D、45°9. 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )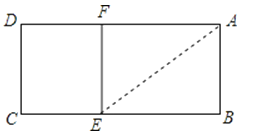 A、 B、 C、4 D、210. 如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图形含有正方形的个数是( )
A、 B、 C、4 D、210. 如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图形含有正方形的个数是( ) A、102 B、91 C、55 D、3111. 如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
A、102 B、91 C、55 D、3111. 如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )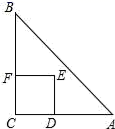 A、
A、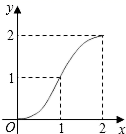 B、
B、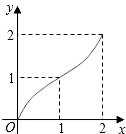 C、
C、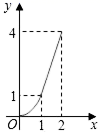 D、
D、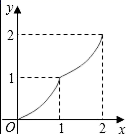 12. 如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图像上,已知点B的坐标是( , ),则k的值为( )
12. 如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图像上,已知点B的坐标是( , ),则k的值为( )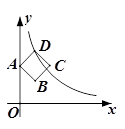 A、10 B、8 C、6 D、4
A、10 B、8 C、6 D、4二、填空题
-
13. 刚刚过去的2015年,中国旅游业实现了持续健康较快的发展,预计全年旅游总收入可达2900000000000元,将数据2900000000000用科学记数法表示为 .14. 请计算:(1+π)0+(﹣ )﹣2+2sin60°﹣| +1|= .15.
如图是由若干个小正方形搭建的几何体的三视图,那么此几何体由 个小正方形搭建而成.
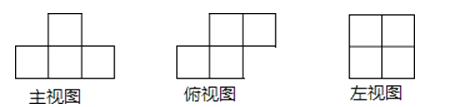 16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB= ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为(结果保留π)
16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB= ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为(结果保留π) 17. 有七张正面分别标有数字-3,-2,-1,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于 的一元二次方程 有两个不相等的实数根,且以x为自变量的二次函数 的图象不经过点(1,0)的概率是.18. 如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2 ,则MN的值为.
17. 有七张正面分别标有数字-3,-2,-1,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于 的一元二次方程 有两个不相等的实数根,且以x为自变量的二次函数 的图象不经过点(1,0)的概率是.18. 如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2 ,则MN的值为.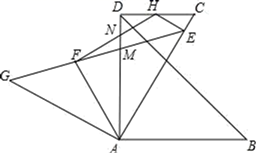
三、解答题
-
19. 解方程: .20. 如图,在△ABC中,∠ABC=∠ACB,过A作AD⊥AB交BC的延长线于点D,过点C作CE⊥AC,使AE=BD.求证:∠E=∠D.
 21. 化简下列各式:(1)、 ;(2)、 .22. 某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:
21. 化简下列各式:(1)、 ;(2)、 .22. 某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:测试成绩频数分布表
组别
成绩x次
频数(人数)
频率
A
100≤x<120
5
B
120≤x<140
b
C
140≤x<160
15
30%
D
160≤x<180
10
E
180≤x<200
a
 (1)、填空:a= , b= , 本次跳绳测试成绩的中位数落在组(请填写字母);(2)、补全频数分布直方图;(3)、已知本班中甲、乙两位同学的测试成绩分别为185次、195次,现要从E组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中至少1人被选中的概率.23. 对x,y定义一种新运算T,规定 (其中a,b均为非零常数),这里等式右边是通常的四则运算,例: .
(1)、填空:a= , b= , 本次跳绳测试成绩的中位数落在组(请填写字母);(2)、补全频数分布直方图;(3)、已知本班中甲、乙两位同学的测试成绩分别为185次、195次,现要从E组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中至少1人被选中的概率.23. 对x,y定义一种新运算T,规定 (其中a,b均为非零常数),这里等式右边是通常的四则运算,例: .已知 , .
(1)、求a,b的值;(2)、若关于m的不等式组 恰好有3个整数解,求实数p的取值范围.24. 如图,我国某边防哨所树立了“祖国在我心中”建筑物,它的横截面为四边形BCNM,其中BC⊥CN,BM∥CN,建筑物顶上有一旗杆AB,士兵小明站在D处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,已知旗杆AB=2.8米,DE=1.8米.(参考数据:sin52°≈0.788,tan52°≈1.280)
 (1)、求建筑物的高度BC;(2)、建筑物长50米,背风坡MN的坡度i=1:0.5,为提高建筑物抗风能力,士兵们在背风坡填筑土石方加固,加固后建筑物顶部加宽4.2米,背风坡GH的坡度为i=1:1.5,施工10天后,边防居民为士兵支援的机械设备终于到达,这样工作效率提高到了原来的2倍,结果比原计划提前20天完成加固任务,士兵们原计划平均每天填筑土石方多少立方米?
(1)、求建筑物的高度BC;(2)、建筑物长50米,背风坡MN的坡度i=1:0.5,为提高建筑物抗风能力,士兵们在背风坡填筑土石方加固,加固后建筑物顶部加宽4.2米,背风坡GH的坡度为i=1:1.5,施工10天后,边防居民为士兵支援的机械设备终于到达,这样工作效率提高到了原来的2倍,结果比原计划提前20天完成加固任务,士兵们原计划平均每天填筑土石方多少立方米?
25. 如图1,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,过点C作CF⊥CP交于C,交AB于点F,过点B作BM⊥CF于点N,交AC于点M. (1)、若AP= AC,BC=4,求S△ACP;(2)、若CP﹣BM=2FN,求证:BC=MC;(3)、如图2,在其他条件不变的情况下,将“正方形ABCD”改为“矩形ABCD”,且AB≠BC,AC=AP,取CP中点E,连接EB,交AC于点O,猜想:∠AOB与∠ABM之间有何数量关系?请说明理由.26. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c分别交 x轴于A(4,0)、B(1,0),交y轴于点C(0,﹣3),过点A的直线 交抛物线与另一点D.
(1)、若AP= AC,BC=4,求S△ACP;(2)、若CP﹣BM=2FN,求证:BC=MC;(3)、如图2,在其他条件不变的情况下,将“正方形ABCD”改为“矩形ABCD”,且AB≠BC,AC=AP,取CP中点E,连接EB,交AC于点O,猜想:∠AOB与∠ABM之间有何数量关系?请说明理由.26. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c分别交 x轴于A(4,0)、B(1,0),交y轴于点C(0,﹣3),过点A的直线 交抛物线与另一点D. (1)、求抛物线的解析式及点D的坐标;(2)、若点P为x轴上的一个动点,点Q在线段AC上,且Q点到x轴的距离为 ,连接PC、PQ,当△PCQ周长最小时,求出点P的坐标;(3)、如图2,在(2)的结论下,连接PD,在平面内是否存在△A1P1D1 , 使△A1P1D1≌△APD(点A1、P1、D1的对应点分别是A、P、D,A1P1平行于y轴,点P1在点A1上方),且△A1P1D1的两个顶点恰好落在抛物线上?若存在,请求出点A1的横坐标m;若不存在,请说明理由.
(1)、求抛物线的解析式及点D的坐标;(2)、若点P为x轴上的一个动点,点Q在线段AC上,且Q点到x轴的距离为 ,连接PC、PQ,当△PCQ周长最小时,求出点P的坐标;(3)、如图2,在(2)的结论下,连接PD,在平面内是否存在△A1P1D1 , 使△A1P1D1≌△APD(点A1、P1、D1的对应点分别是A、P、D,A1P1平行于y轴,点P1在点A1上方),且△A1P1D1的两个顶点恰好落在抛物线上?若存在,请求出点A1的横坐标m;若不存在,请说明理由.