甘肃省酒泉市瓜州县2020年数学中考一模试卷
试卷更新日期:2020-07-28 类型:中考模拟
一、选择题
-
1. 下列图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列根式中是最简二次根式的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、a3•a3=2a3 B、a3÷a=a3 C、a+a=2a D、(a3)2=a54. 不等式组 的解集是( )A、 B、 C、 D、5. 天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )A、 B、 C、 D、6. 如图的几何体是由一个正方体切去一个小正方体形成的,它的主视图是( )
2. 下列根式中是最简二次根式的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、a3•a3=2a3 B、a3÷a=a3 C、a+a=2a D、(a3)2=a54. 不等式组 的解集是( )A、 B、 C、 D、5. 天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )A、 B、 C、 D、6. 如图的几何体是由一个正方体切去一个小正方体形成的,它的主视图是( )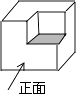 A、
A、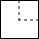 B、
B、 C、
C、 D、
D、 7. 若正多边形的内角和是540°,则该正多边形的一个外角为( )
7. 若正多边形的内角和是540°,则该正多边形的一个外角为( )
A、45° B、60° C、72° D、90°8. A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )A、 B、 C、+4=9 D、9. 如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( ) A、3 B、4 C、5 D、610. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A、3 B、4 C、5 D、610. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )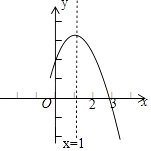 A、①②④ B、①②⑤ C、②③④ D、③④⑤
A、①②④ B、①②⑤ C、②③④ D、③④⑤二、填空题
-
11. 分解因式: .12. 使得代数式 有意义的 的取值范围是 .
13. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是 .14. 已知双曲线 经过点 ,则 .15. 中国“一带一路”给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均年收入20000元,到2018年人均年收入达到39200元.则该地区居民年人均收入平均增长率为.(用百分数表示)16. 如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα= , 则t的值是 17. 如图,在⊙O中,弦AC=2 ,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=.
17. 如图,在⊙O中,弦AC=2 ,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=. 18. 如图图形都是由完全相同的小梯形按一定的规律组成的,如果第1个图形的周长为5,那么第2个图形的周长为 , 第2020个图形的周长为.
18. 如图图形都是由完全相同的小梯形按一定的规律组成的,如果第1个图形的周长为5,那么第2个图形的周长为 , 第2020个图形的周长为.
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中x=﹣5.21. 美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
 22. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,按要求完成下列步骤:
22. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,按要求完成下列步骤: (1)、①画出将△ABC向上平移3个单位后得到的△A1B1C1;
(1)、①画出将△ABC向上平移3个单位后得到的△A1B1C1;②画出将△A1B1C1绕点C1按顺时针方向旋转90°后所得到的△A2B2C1.
(2)、求出第(1)②问中B1点经过的路径长.23. 为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.(1)、小明从中随机抽取一张卡片是足球社团B的概率是.(2)、小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.24. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
七年级
0
1
0
a
7
1
八年级
1
0
0
7
b
2
分析数据:
平均数
众数
中位数
七年级
78
75
八年级
78
80.5
应用数据:
(1)、由上表填空:a= , b= , c= , d=.(2)、估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?(3)、你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.25. 如图,已知反比例函数y= (x>0)的图象与一次函数y=﹣ x+4的图象交于A和B(6,n)两点.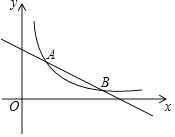 (1)、求k和n的值;
(1)、求k和n的值;
(2)、若点C(x,y)也在反比例函数y= (x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.26. 如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.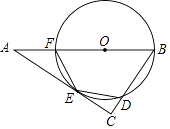 (1)、求证:∠C=90°;(2)、当BC=3,sinA= 时,求AF的长.27. 某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)、求证:∠C=90°;(2)、当BC=3,sinA= 时,求AF的长.27. 某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q. (1)、求证:DP=DQ;(2)、如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)、如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.28. 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
(1)、求证:DP=DQ;(2)、如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)、如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.28. 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M. (1)、求此抛物线的解析式和对称轴;(2)、在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(1)、求此抛物线的解析式和对称轴;(2)、在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.