天津市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 计算 的结果等于( )A、10 B、-10 C、50 D、-502. 2sin45°的值等于()A、1 B、 C、 D、23. 据2020年6月24日《天津日报》报道,6月23日下午,第四届世界智能大会在天津开幕.本届大会采取“云上”办会的全新模式呈现,40家直播网站及平台同时在线观看云开幕式暨主题峰会的总人数最高约为58600000人.将58600000用科学记数法表示应为( )A、 B、 C、 D、4. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
5. 下图是一个由5个相同的正方体组成的立体图形,它的主视图是( )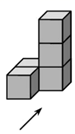 A、
A、 B、
B、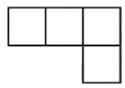 C、
C、 D、
D、 6. 估计 的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间7. 方程组 的解是( )A、 B、 C、 D、8. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )
6. 估计 的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间7. 方程组 的解是( )A、 B、 C、 D、8. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )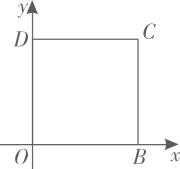 A、 B、 C、 D、9. 计算 的结果是( )A、 B、 C、1 D、10. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,在 中, ,将 绕点C顺时针旋转得到 ,使点B的对应点E恰好落在边 上,点A的对应点为D , 延长 交 于点F , 则下列结论一定正确的是( )
A、 B、 C、 D、9. 计算 的结果是( )A、 B、 C、1 D、10. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,在 中, ,将 绕点C顺时针旋转得到 ,使点B的对应点E恰好落在边 上,点A的对应点为D , 延长 交 于点F , 则下列结论一定正确的是( ) A、 B、 C、 D、12. 已知抛物线 ( 是常数, )经过点 ,其对称轴是直线 .有下列结论:
A、 B、 C、 D、12. 已知抛物线 ( 是常数, )经过点 ,其对称轴是直线 .有下列结论:① ;②关于x的方程 有两个不等的实数根;③ .其中,正确结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
13. 计算 的结果等于 .14. 计算 的结果等于 .15. 不透明袋子中装有8个球,其中有3个红球、5个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .16. 将直线 向上平移1个单位长度,平移后直线的解析式为 .17. 如图, 的顶点C在等边 的边 上,点E在 的延长线上,G为 的中点,连接 .若 , ,则 的长为 .
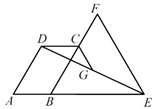 18. 如图,在每个小正方形的边长为1的网格中, 的顶点 均落在格点上,点B在网格线上,且 .
18. 如图,在每个小正方形的边长为1的网格中, 的顶点 均落在格点上,点B在网格线上,且 . (1)、线段 的长等于;(2)、以 为直径的半圆与边 相交于点D , 若 分别为边 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .
(1)、线段 的长等于;(2)、以 为直径的半圆与边 相交于点D , 若 分别为边 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .20. 农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
(4)、原不等式组的解集为 .20. 农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
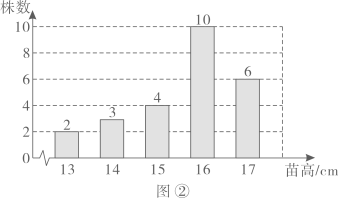
请根据相关信息,解答下列问题:
(1)、本次抽取的麦苗的株数为 , 图①中m的值为;(2)、求统计的这组苗高数据的平均数、众数和中位数.21. 在 中,弦 与直径 相交于点P , .
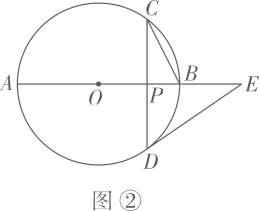 (1)、如图①,若 ,求 和 的大小;(2)、如图②,若 ,过点D作 的切线,与 的延长线相交于点E , 求 的大小.22. 如图, 两点被池塘隔开,在 外选一点C , 连接 .测得 , , .根据测得的数据,求 的长(结果取整数).
(1)、如图①,若 ,求 和 的大小;(2)、如图②,若 ,过点D作 的切线,与 的延长线相交于点E , 求 的大小.22. 如图, 两点被池塘隔开,在 外选一点C , 连接 .测得 , , .根据测得的数据,求 的长(结果取整数).参考数据: , , .
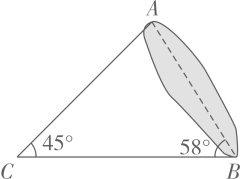 23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.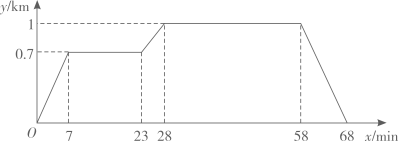
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
0.7
(2)、填空:①食堂到图书馆的距离为 .
②小亮从食堂到图书馆的速度为 .
③小亮从图书馆返回宿舍的速度为 .
④当小亮离宿舍的距离为 时,他离开宿舍的时间为 .
(3)、当 时,请直接写出y关于x的函数解析式.24. 将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点B在第一象限, , ,点P在边 上(点P不与点 重合).
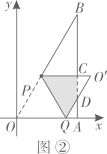 (1)、如图①,当 时,求点P的坐标;(2)、折叠该纸片,使折痕所在的直线经过点P , 并与x轴的正半轴相交于点Q , 且 ,点O的对应点为 ,设 .
(1)、如图①,当 时,求点P的坐标;(2)、折叠该纸片,使折痕所在的直线经过点P , 并与x轴的正半轴相交于点Q , 且 ,点O的对应点为 ,设 .①如图②,若折叠后 与 重叠部分为四边形, 分别与边 相交于点 ,试用含有t的式子表示 的长,并直接写出t的取值范围;
②若折叠后 与 重叠部分的面积为S , 当 时,求S的取值范围(直接写出结果即可).
25. 已知点 是抛物线 ( 为常数, )与x轴的一个交点.(1)、当 时,求该抛物线的顶点坐标;(2)、若抛物线与x轴的另一个交点为 ,与y轴的交点为C , 过点C作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点, .①当点E落在抛物线上(不与点C重合),且 时,求点F的坐标;
②取 的中点N , 当m为何值时, 的最小值是 ?