四川省遂宁市2020年中考数学试卷

试卷更新日期：2020-07-28 类型：中考真卷

进入出卷网下载

一、单选题

1. －5的相反数是（）

A、-5 B、5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示为（）

A、8.23×10^﹣⁶ B、8.23×10^﹣⁷ C、8.23×10⁶ D、8.23×10⁷

查看试题解析
3. 下列计算正确的是（）

A、7ab﹣5a＝2b B、（a+ $\frac{1}{a}$ ）²＝a²+ $\frac{1}{a^{2}}$ C、（﹣3a²b）²＝6a⁴b² D、3a²b÷b＝3a²

查看试题解析
4. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、等边三角形 B、平行四边形 C、矩形 D、正五边形

查看试题解析
5. 函数y＝ $\frac{\sqrt{x + 2}}{x - 1}$ 中，自变量x的取值范围是（）

A、x＞﹣2 B、x≥﹣2 C、x＞﹣2且x≠1 D、x≥﹣2且x≠1

查看试题解析
6. 关于x的分式方程 $\frac{m}{x - 2}$ ﹣ $\frac{3}{2 - x}$ ＝1有增根，则m的值（）

A、m＝2 B、m＝1 C、m＝3 D、m＝﹣3

查看试题解析
7. 如图，在平行四边形ABCD中，∠ABC的平分线交AC于点E ，交AD于点F ，交CD的延长线于点G ，若AF＝2FD ，则 $\frac{B E}{E G}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
8. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，对称轴为直线x＝﹣1，下列结论错误的是（）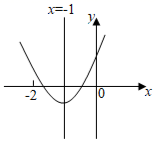

A、b²＞4ac B、abc＞0 C、a﹣c＜0 D、am²+bm≥a﹣b（m为任意实数）

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，AC＝BC ，点O在AB上，经过点A的⊙O与BC相切于点D ，交AB于点E ，若CD＝ $\sqrt{2}$ ，则图中阴影部分面积为（）

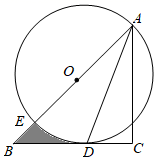A、4﹣ $\frac{π}{2}$ B、2﹣ $\frac{π}{2}$ C、2﹣π D、1﹣ $\frac{π}{4}$

查看试题解析
10. 如图，在正方形ABCD中，点E是边BC的中点，连接AE、DE ，分别交BD、AC于点P、Q ，过点P作PF⊥AE交CB的延长线于F ，下列结论：
①∠AED+∠EAC+∠EDB＝90°，②AP＝FP ， ③AE＝ $\frac{\sqrt{10}}{2}$ AO ， ④若四边形OPEQ的面积为4，则该正方形ABCD的面积为36，⑤CE•EF＝EQ•DE ．

其中正确的结论有（）

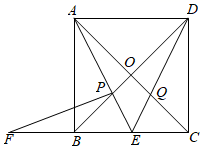A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

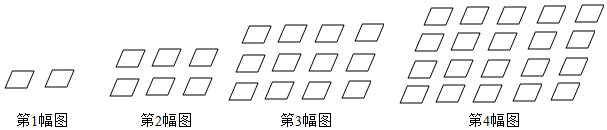
11. 下列各数3.1415926， $\sqrt{9}$ ，1.212212221…， $\frac{1}{7}$ ，2﹣π，﹣2020， $\sqrt[3]{4}$ 中，无理数的个数有个．

查看试题解析
12. 一列数4、5、4、6、x、5、7、3中，其中众数是4，则x的值是．

查看试题解析
13. 已知一个正多边形的内角和为1440°，则它的一个外角的度数为度．

查看试题解析
14. 若关于x的不等式组 ${\begin{array}{l} \frac{x - 2}{4} < \frac{x - 1}{3} \\ 2 x - m \leq 2 - x \end{array}$ 有且只有三个整数解，则m的取值范围是．

查看试题解析
15. 如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形，第1幅图中“▱”的个数为a₁ ，第2幅图中“▱”的个数为a₂ ，第3幅图中“▱”的个数为a₃ ， …，以此类推，若 $\frac{2}{a_{1}}$ + $\frac{2}{a_{2}}$ + $\frac{2}{a_{3}}$ +…+ $\frac{2}{a_{n}}$ ＝ $\frac{n}{2020}$ ．（n为正整数），则n的值为．

查看试题解析

三、解答题

16. 计算： $\sqrt{8}$ ﹣2sin30°﹣|1﹣ $\sqrt{2}$ |+（ $\frac{1}{2}$ ）^﹣²﹣（π﹣2020）⁰ ．

查看试题解析
17. 先化简，（ $\frac{x^{2} + 4 x + 4}{x^{2} - 4}$ ﹣x﹣2）÷ $\frac{x + 2}{x - 2}$ ，然后从﹣2≤x≤2范围内选取一个合适的整数作为x的值代入求值．

查看试题解析
18. 如图，在△ABC中，AB＝AC ，点D、E分别是线段BC、AD的中点，过点A作BC的平行线交BE的延长线于点F ，连接CF ．

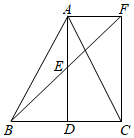(1)、求证：△BDE≌△FAE；

(2)、求证：四边形ADCF为矩形．

查看试题解析
19. 在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践，如图为实践时绘制的截面图．无人机从地面点B垂直起飞到达点A处，测得1号楼顶部E的俯角为67°，测得2号楼顶部F的俯角为40°，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且EC和FD分别垂直地面于点C和D ，点B为CD的中点，求2号楼的高度．（结果精确到0.1）（参考数据sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

查看试题解析
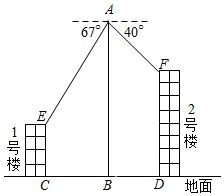20. 新学期开始时，某校九年级一班的同学为了增添教室绿色文化，打造温馨舒适的学习环境，准备到一家植物种植基地购买A、B两种花苗．据了解，购买A种花苗3盆，B种花苗5盆，则需210元；购买A种花苗4盆，B种花苗10盆，则需380元．

(1)、求A、B两种花苗的单价分别是多少元？

(2)、经九年级一班班委会商定，决定购买A、B两种花苗共12盆进行搭配装扮教室．种植基地销售人员为了支持本次活动，为该班同学提供以下优惠：购买几盆B种花苗，B种花苗每盆就降价几元，请你为九年级一班的同学预算一下，本次购买至少准备多少钱？最多准备多少钱？

查看试题解析
21. 阅读以下材料，并解决相应问题：
小明在课外学习时遇到这样一个问题：

定义：如果二次函数y＝a₁x²+b₁x+c₁（a₁≠0，a₁、b₁、c₁是常数）与y＝a₂x²+b₂x+c₂（a₂≠0，a₂、b₂、c₂是常数）满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则这两个函数互为“旋转函数”．求函数y＝2x²﹣3x+1的旋转函数，小明是这样思考的，由函数y＝2x²﹣3x+1可知，a₁＝2，b₁＝﹣3，c₁＝1，根据a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，求出a₂ ， b₂ ， c₂就能确定这个函数的旋转函数．

请思考小明的方法解决下面问题：

(1)、写出函数y＝x²﹣4x+3的旋转函数．

(2)、已知函数y＝2（x﹣1）（x+3）的图象与x轴交于A、B两点，与y轴交于点C ，点A、B、C关于原点的对称点分别是A₁、B₁、C₁ ，试求证：经过点A₁、B₁、C₁的二次函数与y＝2（x﹣1）（x+3）互为“旋转函数”．

查看试题解析
22. 端午节是中国的传统节日．今年端午节前夕，遂宁市某食品厂抽样调查了河东某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况，并将调查情况绘制成如图两幅不完整统计图：

(1)、本次参加抽样调查的居民有人．

(2)、喜欢C种口味粽子的人数所占圆心角为度．根据题中信息补全条形统计图．

(3)、若该居民小区有6000人，请你估计爱吃D种粽子的有人．

(4)、若有外型完全相同的A、B、C、D棕子各一个，煮熟后，小李吃了两个，请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率．

查看试题解析
23. 如图，在平面直角坐标系中，已知点A的坐标为（0，2），点B的坐标为（1，0），连结AB ，以AB为边在第一象限内作正方形ABCD ，直线BD交双曲线y═ $\frac{k}{x}$ （k≠0）于D、E两点，连结CE ，交x轴于点F ．

(1)、求双曲线y＝ $\frac{k}{x}$ （k≠0）和直线DE的解析式．

(2)、求 $△ D E C$ 的面积．

查看试题解析
24. 如图，在Rt△ABC中，∠ACB＝90°，D为AB边上的一点，以AD为直径的⊙O交BC于点E ，交AC于点F ，过点C作CG⊥AB交AB于点G ，交AE于点H ，过点E的弦EP交AB于点Q（EP不是直径），点Q为弦EP的中点，连结BP ， BP恰好为⊙O的切线．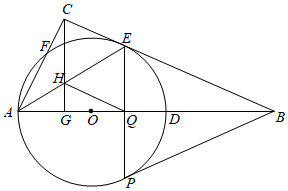

(1)、求证：BC是⊙O的切线．

(2)、求证： $\overset{⌢}{E F}$ ＝ $\overset{⌢}{E D}$ ．

(3)、若sin∠ABC═ $\frac{3}{5}$ ，AC＝15，求四边形CHQE的面积．

查看试题解析
25. 如图，抛物线y＝ax²+bx+c（a≠0）的图象经过A（1，0），B（3，0），C（0，6）三点．

(1)、求抛物线的解析式．

(2)、抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D ，直线BE交AD于点E ，若直线BE将△ABD的面积分为1：2两部分，求点E的坐标．

(3)、P为抛物线上的一动点，Q为对称轴上动点，抛物线上是否存在一点P ，使A、D、P、Q为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析