浙江省台州市椒江区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-28 类型：期末考试

进入出卷网下载

一、选择题

1. 如图，直线a，b相交于点O，∠1＝60°，则∠2＝（）

A、120° B、60° C、30° D、15°

查看试题解析
2. 下列实数中是无理数的是（）

A、 $\sqrt{4}$ B、0.212121 C、 $\sqrt{2}$ D、﹣ $\frac{10}{3}$

查看试题解析
3. 下列调查方式中，你认为最合适的是（）

A、肺炎疫情期间，对学生体温测量采用抽样调查 B、驰援武汉医疗队胜利归来时，为了确定医疗队成员的健康情况，可采用抽样调查 C、检查一批口罩的防护效果时，采用全面调查 D、肺炎疫情期间到校上课，了解学生健康码情况时，采用全面调查

查看试题解析
4. 下列命题中，是假命题的为（）

A、两直线平行，同旁内角相等 B、两直线平行，内错角相等 C、同位角相等，两直线平行 D、同旁内角互补，两直线平行

查看试题解析
5. 如图，数轴上点A表示的数可能是（）

A、﹣ $\sqrt{5}$ B、﹣ $\sqrt{10}$ C、﹣ $\sqrt{17}$ D、﹣ $\sqrt[3]{65}$

查看试题解析
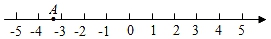6. 如图形中，周长最长的是（）

A、 B、 C、 D、

查看试题解析
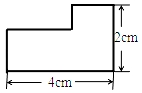7. 一副三角尺按如图方式叠放，含30°角三角形尺的直角边AD在含45°角三角形尺的直角边AC上，则∠BFE的度数是（）

A、60° B、70° C、75° D、80°

查看试题解析
8. 某校网课学习的要求是每周听课时长至少达到480分钟算合格.张飞前3天平均每天听课时长为90分钟，问张飞后2天平均每天听课时长不得少于多少分钟才能合格？设张飞后2天平均听课时长为x分钟，以下所列不等式正确的是（）

A、90×3+2x≥480 B、90×3+2x≤480 C、90×3+2x＜480 D、90×3+2x≥480

查看试题解析
9. 如图，用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案，已知A（﹣2，6），则点B的坐标为（）

A、（﹣6，4） B、（ $- \frac{20}{3}$ ， $\frac{14}{3}$ ） C、（﹣6，5） D、（ $- \frac{20}{3}$ ，4）

查看试题解析
10. 在平面直角坐标系中，点M（1+m，2m﹣3）不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、填空题（本题有6小题，每小题3分18分）

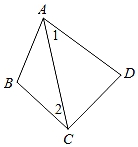
11. 小红在画一组数据的直方图时，统计了这组数据中的最大值是75，最小值是4，她准备把这组数据分成8组，则组距可设为.（填一整数）

查看试题解析
12. 如图，∠1＝∠2，∠D＝75°，则∠BCD＝.

查看试题解析
13. 若 $\sqrt{3}$ ≈1.732，则300的平方根约为.

查看试题解析
14. 若 $\sqrt{x + 2 y - 3} + {(2 x + y - 3)}^{2}$ ＝0，则x+y的值为.

查看试题解析
15. 已知a+b＝4，若﹣2≤b≤﹣1，则a的取值范围是.

查看试题解析
16. 在平面直角坐标系xOy中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P的伴随点.已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得点A₁ ， A₂ ， A₃…，A_n ， …若点A₁的坐标为（3，1），则点A₂₀₁₉的坐标为.

查看试题解析

三、解答题（本题有8小题，第17～20题每题5分，第21题6分，第22，23题每题8，第24题10分，共52分）

17. 计算： $\sqrt{100} + \sqrt[3]{- 8}$ .

查看试题解析
18. 解不等式组 ${\begin{cases} 2 x + 1 \geq - 3 \\ x + 1 > 2 x - 2 \end{cases}$ ，并把它的解集在数轴上表示出来.

查看试题解析
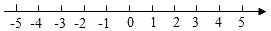19. 如图，在三角形ABC中，AB∥DE，∠BDE＝2∠A，求证∠A＝∠C.
证明：作∠BDE的角平分线交AB于点F.

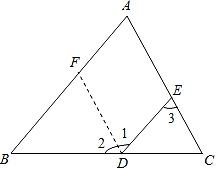
∵DF平分∠BDE，

∴∠1＝∠2.

∵∠BDE＝2∠A，

∴∠1＝∠2＝__▲__，

∵AB∥DE，

∴∠A＝∠3 （_▲_），

∴∠3＝∠A＝_▲_，

∴AC∥DF （_▲_），

∴∠2＝_▲_，

∴∠A＝∠C＝∠2.

查看试题解析

20. 某校为了提高学生的实践能力，开展了手工制作比赛.已知参赛作品分数记为x分（60≤x≤100），校方在参赛作品中随机抽取了50件作品进行质量评估，分数情况统计表和统计图如图所示：

手工制作比赛作品分数情况频数分布表手工制作比赛作品分数情况频数分布直方图根据以上信息解答下列问题：

手工制作比赛作品分数情况频数分布表

分数段	频数	频率
60≤x＜70	15	0.3
70≤x＜80	22	c
80≤x＜90	a	0.2
90≤x≤100	b	0.06
合计	50	1

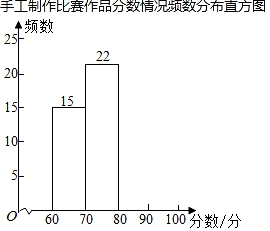(1)、频数分布表中c的值为；

(2)、补全频数分布直方图；

(3)、本次比赛校方共收到参赛作品800件，若80分以上（含80分）的作品将被展出，试估计全校将展出的作品数量.

查看试题解析

21. 如图，AB∥CD，AB∥GE，∠B＝110°，∠C＝100°.∠BFC等于多少度？为什么？

查看试题解析
22. 肺炎疫情期间，口罩成了家家户户必备的防疫物品.在某超市购买2只普通医用口罩和3只N95口罩的费用是22元；购买5只普通医用口罩和2只N95口罩的费用也是22元.

(1)、求该超市普通医用口罩和N95口罩的单价；

(2)、若准备在该超市购买两种口罩共50只，且N95口罩不少于总数的40%，试通过计算说明，在预算不超过190元的情况下有哪些购买方案.

查看试题解析
23. 规定min（m，n）表示m，n中较小的数（m，n均为实数，且mn），例如：min{3，﹣1}＝﹣1，、min ${\sqrt{2} ， \sqrt{3}} = \sqrt{2}$ 据此解决下列问题：

(1)、min ${- \frac{1}{2} ， - \frac{1}{3}}$ ＝；

(2)、若min ${\frac{2 x - 1}{3} ， 2}$ ＝2，求x的取值范围；

(3)、若min{2x﹣5，x+3}＝﹣2，求x的值.

查看试题解析
24. 在平面直角坐标系xOy中，对于给定的两点P，Q，若存在点M，使得△MPQ（△表示三角形）面积等于1（即S_△MPQ＝1），则称点M为线段PQ的“单位面积点”.
解答下列问题：

如图，在平面直角坐标系xOy中，点P的坐标为（2，0）.

(1)、在点A（﹣1，1），B（﹣1，2），C（2，﹣4）中，线段OP的“单位面积点”是；

(2)、已知点D（0，3），E（0，4），将线段OP沿y轴方向向上平移t（t＞0）个单位长度，使得线段DE上存在线段OP的“单位面积点”，求t的取值范围；

(3)、已知点F（2，2），点M在第一象限且M的纵坐标是3，点M，N是线段PF的两个“单位面积点”，若S_△OMN＝3S_△PFN ，且MN∥PF，直接写出点N的坐标.

查看试题解析