四川省泸州市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 2的倒数是( )。A、2 B、 C、 D、-22. 将867000用科学记数法表示为( )A、 B、 C、 D、3. 如下图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、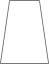 D、
D、 4. 在平面直角坐标系中,将点 向右平移4个单位长度,得到的对应点 的坐标为( )A、 B、 C、 D、5. 下列正多边形中,不是中心对称图形的是( )A、
4. 在平面直角坐标系中,将点 向右平移4个单位长度,得到的对应点 的坐标为( )A、 B、 C、 D、5. 下列正多边形中,不是中心对称图形的是( )A、 B、
B、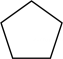 C、
C、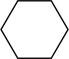 D、
D、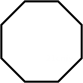 6. 下列各式运算正确的是( )A、 B、 C、 D、7. 如图, 中, , .则 的度数为( )
6. 下列各式运算正确的是( )A、 B、 C、 D、7. 如图, 中, , .则 的度数为( )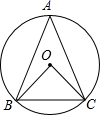 A、100° B、90° C、80° D、70°8. 某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如下表所示:
A、100° B、90° C、80° D、70°8. 某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如下表所示:课外阅读时间(小时) 0.5 1 1.5 2 人数 2 3 4 1 那么这10名学生平均每天的课外阅读时间的平均数和众数分别是( )
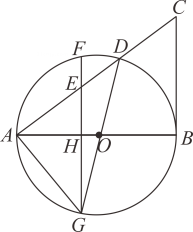
A、1.2和1.5 B、1.2和4 C、1.25和1.5 D、1.25和49. 下列命题是假命题的是( )A、平行四边形的对角线互相平分 B、矩形的对角线互相垂直 C、菱形的对角线互相垂直平分 D、正方形的对角线互相垂直平分且相等10. 已知关于x的分式方程 的解为非负数,则正整数m的所有个数为( )A、3 B、4 C、5 D、611. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )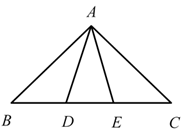 A、 B、 C、 D、12. 已知二次函数 (其中x是自变量)的图象经过不同两点 , ,且该二次函数的图象与x轴有公共点,则 的值( )A、-1 B、2 C、3 D、4
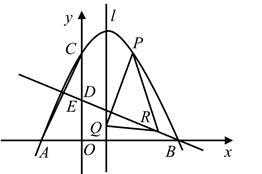
A、 B、 C、 D、12. 已知二次函数 (其中x是自变量)的图象经过不同两点 , ,且该二次函数的图象与x轴有公共点,则 的值( )A、-1 B、2 C、3 D、4二、填空题
-
13. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .14. 若 与 是同类项,则a的值是 .15. 已知 是一元二次方程 的两个实数根,则 的值是 .16. 如图,在矩形 中, 分别为边 , 的中点, 与 , 分别交于点M , N . 已知 , ,则 的长为 .

三、解答题
-
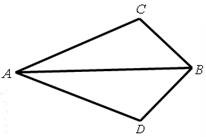
17. 计算: .18. 如图,AB平分∠CAD,AC=AD.求证:BC=BD.
 19. 化简: .20. 某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
19. 化简: .20. 某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.根据题中已有信息,解答下列问题:
 (1)、求n的值,并补全频数分布直方图;(2)、若该汽车公司有600辆该型号汽车,试估计耗油 所行使的路程低于 的该型号汽车的辆数;(3)、从被抽取的耗油 所行使路程在 , 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.21. 某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.(1)、如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?(2)、若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?22. 如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于A , B两点.且点A的坐标为 .
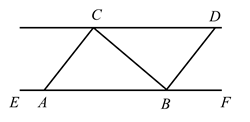
(1)、求n的值,并补全频数分布直方图;(2)、若该汽车公司有600辆该型号汽车,试估计耗油 所行使的路程低于 的该型号汽车的辆数;(3)、从被抽取的耗油 所行使路程在 , 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.21. 某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.(1)、如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?(2)、若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?22. 如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于A , B两点.且点A的坐标为 .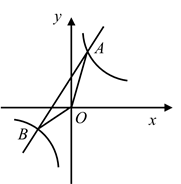 (1)、求该一次函数的解析式;(2)、求 的面积.23. 如图,为了测量某条河的对岸边C , D两点间的距离,在河的岸边与 平行的直线 上取两点A , B , 测得 , ,量得 长为70米.求C , D两点间的距离(参考数据: , , ).
(1)、求该一次函数的解析式;(2)、求 的面积.23. 如图,为了测量某条河的对岸边C , D两点间的距离,在河的岸边与 平行的直线 上取两点A , B , 测得 , ,量得 长为70米.求C , D两点间的距离(参考数据: , , ).