浙江省绍兴市越城区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-28 类型：期末考试

进入出卷网下载

一、选择题（共10小题）.

1. 下列各式中，化简后能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{12}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{0.2}$

查看试题解析
2. 一元二次方程x²﹣2x=0的两根分别为x₁和x₂ ，则x₁x₂为（　　）

A、﹣2 B、1 C、2 D、0

查看试题解析
3. 已知反比例函数的图象过点M（﹣1，2），则此反比例函数的表达式为（）

A、y＝ $\frac{2}{x}$ B、y＝﹣ $\frac{2}{x}$ C、y＝ $\frac{1}{2 x}$ D、y＝﹣ $\frac{1}{2 x}$

查看试题解析
4. 有一组数椐：3，4，5，6，6，则下列四个结论中正确的是（）

A、这组数据的平均数、众数、中位数分别是4.8，6，6 B、这组数据的平均数、众数、中位数分别是5，5，5 C、这组数据的平均数、众数、中位数分别是4.8，6，5 D、这组数据的平均数、众数、中位数分别是5，6，6

查看试题解析
5. 已知▱ABCD中，∠A+∠C＝80°，则∠B的度数为（）

A、80° B、100° C、120° D、140°

查看试题解析
6. 估算 $\sqrt{31} - 2$ 的值（）

A、在 $1$ 和 $2$ 之间 B、在 $2$ 和 $3$ 之间 C、在 $3$ 和 $4$ 之间 D、在 $4$ 和 $5$ 之间

查看试题解析
7. 若a，b，c满足 ${\begin{cases} a + b + c = 0 \\ a - b + c = 0 \end{cases}$ ，则关于x的方程ax²+bx+c＝0（a≠0）的解是（）

A、1，0 B、﹣1，0 C、1，﹣1 D、无实数根

查看试题解析
8. 从下列条件中选择一个条件添加后，还不能判定平行四边形ABCD是菱形，则这个条件是（）

A、AC⊥BD B、AC=BD C、AB=BC D、AD=CD

查看试题解析
9. 如图，已知双曲线y＝ $\frac{k}{x}$ （k＜0）经过Rt△OAB斜边OA的中点D，且与直角边AB相交于点C，若点A的坐标为（﹣6，4），则△AOC的面积为（）

A、12 B、10 C、9 D、8

查看试题解析
10. 小明使用图形计算器探究函数y＝ $\frac{a x}{{(x - b)}^{2}}$ 的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（　　）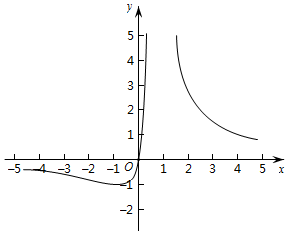

A、a＞0，b＞0 B、a＞0，b＜0 C、a＜0，b＞0 D、a＜0，b＜0

查看试题解析

二、填空题（本大题共6小题，每题3分，共18分）

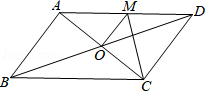
11. 某组数据﹣2，﹣1，0，1，2的方差为.

查看试题解析
12. 若 $\sqrt{x - 8}$ + $\sqrt{y - 2}$ ＝0，则x+y＝.

查看试题解析
13. 如图， $▱$ ABCD的对角线相交于点O，且AD $\neq$ CD，过点O作OM $⊥$ AC，交AD于点M．如果 $△$ CDM的周长为8，那么 $▱$ ABCD的周长是．

查看试题解析
14. 已知x=2是关于x的一元二次方程kx²+（k²﹣2）x+2k+4=0的一个根，则k的值为．

查看试题解析
15. 如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q.若PQ＝AE，则AP等于cm.

查看试题解析
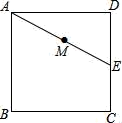16. 如图，曲线l是由函数y＝ $\frac{6}{x}$ 在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（﹣4 $\sqrt{2}$ ，4 $\sqrt{2}$ ），B（2 $\sqrt{2}$ ，2 $\sqrt{2}$ ）的直线与曲线l相交于点M、N，则△OMN的面积为.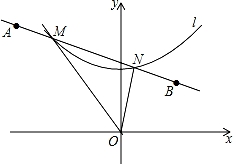

查看试题解析

三、解答题（本大题共52分）

17. 计算：

(1)、4 $\sqrt{3}$ ﹣ $\sqrt{12}$ + $\sqrt{18}$ ；

(2)、 $\sqrt{10}$ （3 $\sqrt{\frac{2}{5}}$ ﹣ $\sqrt{\frac{5}{2}}$ ）.

查看试题解析
18. 选择合适的方法解一元二次方程：

(1)、4（x﹣5）²＝16；

(2)、（x+3）（x﹣1）＝5.

查看试题解析
19. 如图，在▱ABCD中，∠ABD＝90°，延长AB至点E，使BE＝AB，连接CE.求证：四边形BECD是矩形.

查看试题解析
20. 已知图中的曲线是反比例函数y＝ $\frac{m - 5}{x}$ （m为常数）图象的一支.

(1)、根据图象位置，求m的取值范围；

(2)、若该函数的图象任取一点A，过A点作x轴的垂线，垂足为B，当△OAB的面积为4时，求m的值.

查看试题解析
21.
某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后，绘制了如下统计表与条形图：
尺码（码）
数量（双）
百分比（%）
36
60
30
37
30
15
38
a
b
39
40
20
40
c
5
41
10
5

(1)、写出表中a，b，c的值；

(2)、补全条形图.

(3)、商场经理准备购进同一品牌的旅游鞋1500双，请根据市场实际情况估计他应该购进38码的鞋多少双？

查看试题解析
22. 已知关于x的方程mx²+（3m+1）x+3＝0.

(1)、求证：不论m为任何实数，此方程总有实数根；

(2)、若方程mx²+（3m+1）x+3＝0有两个不同的整数根，且m为正整数，求m的值.

查看试题解析
23. 如图，在△ABC中，∠ACB＝90°，∠CAB＝30°，以线段AB为边向外作等边△ABD，点E是线段AB的中点，连接CE并延长交线段AD于点F．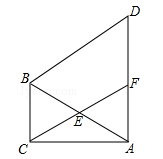

(1)、求证：四边形BCFD为平行四边形；

(2)、若AB＝6，求平行四边形BCFD的面积．

查看试题解析
24. 已知点A、B分别是x轴、y轴上的动点，点C、D是某个函数图象上的点，当四边形ABCD（A、B、C、D各点依次排列）为正方形时，称这个正方形为此函数图象的伴侣正方形.例如：如图，正方形ABCD是一次函数y＝x+1图象的其中一个伴侣正方形.

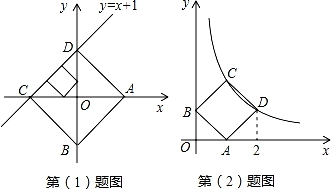(1)、若某函数是一次函数y＝x+1，求它的图象的所有伴侣正方形的边长；

(2)、若某函数是反比例函数 $y = \frac{k}{x} (k > 0)$ ，它的图象的伴侣正方形为ABCD，点D（2，m）（m＜2）在反比例函数图象上，求m的值及反比例函数解析式.

查看试题解析

尺码（码）	数量（双）	百分比（%）
36	60	30
37	30	15
38	a	b
39	40	20
40	c	5
41	10	5