浙江省绍兴市柯桥区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-28 类型：期末考试

进入出卷网下载

一、选择题

1. 在下列英文大写正体字母中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列数化简的结果与实数5不相等的是（）

A、 $\sqrt{5^{2}}$ B、 $\sqrt{{(- 5)}^{2}}$ C、（ $\sqrt{5}$ ）² D、﹣ $\sqrt{{(- 5)}^{2}}$

查看试题解析
3. 已知一元二次方程x²﹣4x+m＝0有一个根为2，则另一根为（）

A、﹣4 B、﹣2 C、4 D、2

查看试题解析
4. 如图，要测量池塘两侧的两点A、B之间的距离，可以取一个能直接到达A、B的点C，连结CA、CB，分别在线段CA、CB上取中点D、E，连结DE，测得DE＝35m，则可得A、B之间的距离为（）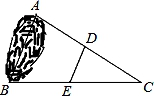

A、30m B、70m C、105m D、140m

查看试题解析
5. 如图，点E在四边形ABCD的CD边的延长线上，若∠ADE＝120°，则∠A+∠B+∠C的度数为（）

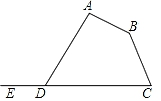A、240° B、260° C、300° D、320°

查看试题解析
6. 如图，在△ABC中，AB＝AC，∠APB≠∠APC，求证：PB≠PC，当用反证法证明时，第一步应假设（）

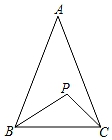A、AB≠AC B、PB＝PC C、∠APB＝∠APC D、∠B≠∠C

查看试题解析
7. 小欣同学对数据36，3■，58，40，62进行统计分析，发现其中一个两位数的个位数字被墨水污染看不到了，则分析结果与被污染数字无关的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
8. 如图所示的▱ABCD，再添加下列某一个条件，不能判定▱ABCD是矩形的是（）

A、AC＝BD B、AB⊥BC C、∠1＝∠2 D、∠ABC＝∠BCD

查看试题解析
9. 小明用四根长度相同的木条首尾相接制作了能够活动的学具，他先活动学具成为图1所示，并测得∠ABC＝60°，接着活动学具成为图2所示，并测得∠ABC＝90°，若图2对角线BD＝20cm，则图1中对角线BD的长为（）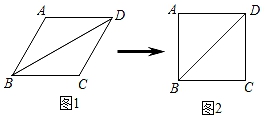

A、10cm B、10 $\sqrt{2}$ cm C、10 $\sqrt{3}$ cm D、10 $\sqrt{6}$ cm

查看试题解析
10. 已知点A在反比例函数y＝ $\frac{k_{1}}{x}$ （x＜0，k₁＜0）的图象上，点B，C在y＝ $\frac{k_{2}}{x}$ （x＞0，k₂＞0）的图象上，AB∥x轴，CD⊥x轴于点D，交AB于点E，若△ABC的面积比△DBC的面积大4， $\frac{C E}{D E}$ ＝ $\frac{2}{3}$ ，则k₁的值为（）

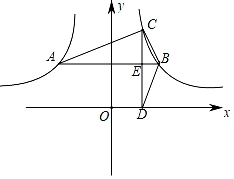A、﹣9 B、﹣12 C、﹣15 D、﹣18

查看试题解析

二、填空题（本题有10小题，每小题3分，共30分）

11. 代数式 $\sqrt{x - 1}$ 中，实数x的取值范围是.

查看试题解析
12. 将方程x（x﹣2）＝x+3化成一般形式后，二次项系数为.

查看试题解析
13. 甲、乙、丙、丁四人各进行了6次跳远测试，他们的平均成绩相同，方差分别是S_甲²＝0.65，S_乙²＝0.55，S_丙²＝0.50，S_丁²＝0.45，则跳远成绩最稳定的是.

查看试题解析
14. 某呼吸机制造商2020年一月份生产呼吸机1000台，2020年三月份生产呼吸机4000台，设二、三月份每月的平均增长率为x，根据题意，可列方程为.

查看试题解析
15. 如图，在正方形ABCD中，E为对角线AC上一点，连接EB、ED，延长BE交AD于点F，若∠DEB＝140°，则∠AFE的度数为：°.

查看试题解析
16. 若关于x的方程2x（x﹣1）+mx＝0有两个相等的实数根，则实数m的值为.

查看试题解析
17. 如图，△ABC的三个顶点分别为A（1，2），B（4，2），C（4，4）.若反比例函数y＝ $\frac{k}{x}$ 在第一象限内的图象与△ABC有交点，则k的取值范围是

查看试题解析
18. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若（x﹣1）（mx﹣n）＝0是倍根方程，则 $\frac{2 n}{m}$ 的值为.

查看试题解析
19. 小敏沿对角线折叠一张矩形纸片，发现所得图形是轴对称图形，接着沿所得图形的对称轴再次折叠后，得到的仍是轴对称图形，则小红折叠的矩形纸片的长宽之比为.

查看试题解析
20. 如图，已知在平行四边形ABCD中，AB＝8 $\sqrt{3}$ ，BC＝20，∠A＝60°，P是边AD上一动点，连结PB，将线段PB绕着点P逆时针旋转90°得到线段PQ，若点Q恰好落在平行四边形ABCD的边上，那么AP的值是.

查看试题解析

三、解答题、（本题有7小题，共50分）

21. 计算：

(1)、 $\sqrt{12}$ ﹣3 $\sqrt{8}$ +2 $\sqrt{18}$ ；

(2)、4 $\sqrt{15}$ ×2 $\sqrt{3}$ ÷ $\sqrt{5}$ .

查看试题解析
22. 解方程：

(1)、2（x﹣1）²＝18；

(2)、x²﹣2x＝2x+1.

查看试题解析

23. 某学校对全体学生“新冠肺炎”疫情防控知识的掌握情况进行了线上测试，该测试共有10道题，每题1分，满分10分。该校将七年级一班和二班的成绩进行整理，得到如下信息：

班级	平均数	中位数	众数	优秀率（9分及以上为优秀）
一班	8.62	a	9	62%
二班	8.72	9	b	c

请你结合图表中所给信息，解答下列问题：

(1)、请直接写出a，b，c的值。

(2)、你认为哪个班对疫情防控知识掌握较好，请说明理由（选择两个角度说明推断的合理性）

查看试题解析

24. 在水果销售旺季，某水果店购进一种优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量（千克）与该天的售价x（元/千克）满足的关系为一次函数y＝﹣2x+80.

(1)、某天这种水果的售价为23.5元/千克，求当天该水果的销售量；

(2)、如果某天销售这种水果获利150元，那么该天水果的售价为多少元？

查看试题解析
25. 在▱ABCD中，E，F分别是AB，DC上的点，且AE＝CF，连接DE，BF，
AF.

(1)、求证：四边形DEBF是平行四边形；

(2)、若AF平分∠DAB，AE＝3，DE＝4，BE＝5，求AF的长.

查看试题解析
26. 如图，在平面直角坐标系xOy中，已知点A坐标（2，3），过点A作AH⊥x轴，垂足为点H ， AH交反比例函数在第一象限的图象于点B ，且满足 $\frac{A B}{B H}$ ＝2．

(1)、求该反比例函数的解析式；

(2)、点C在x正半轴上，点D在该反比例函数的图象上，且四边形ABCD是平行四边形，求点D坐标．

查看试题解析
27. 共顶点的正方形ABCD与正方形AEFG中，AB＝13，AE＝5 $\sqrt{2}$ .

(1)、如图1，求证：DG＝BE；

(2)、如图2，连结BF，以BF、BC为一组邻边作平行四边形BCHF.
①连结BH，BG，求 $\frac{B H}{B G}$ 的值；

②当四边形BCHF为菱形时，直接写出BH的长.

查看试题解析