浙江省宁波市鄞州区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-28 类型：期末考试

进入出卷网下载

一、选择题（共10小题）.

1. 根式 $\sqrt{x - 3}$ 中，x的取值范围是（）

A、x＞3 B、x≥3 C、x＜3 D、x≤3

查看试题解析
2. 平面直角坐标系内，点P（2，﹣3）关于原点对称点的坐标是（　　）

A、（3，﹣2） B、（2，3） C、（2，﹣3） D、（﹣2，3）

查看试题解析
3. 如图，直线l₁∥l₂ ，线段AB的端点A，B分别在直线1₁和1₂上，AB＝6.点C在直线1₂上，∠ABC＝30°，则这两条直线的距离是（）

A、3 B、6 C、2 $\sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析
4. 如图，大坝横截面的迎水坡AB的坡比为1：2，即BC：AC＝1：2，若坡面AB的水平宽度AC为12米，则斜坡AB的长为（）

A、4 $\sqrt{3}$ 米 B、6 $\sqrt{3}$ 米 C、6 $\sqrt{5}$ 米 D、24米

查看试题解析
5. 把一元二次方程（x+3）²＝x（3x﹣1）化成一般形式，正确的是（）

A、2x²﹣7x﹣9＝0 B、2x²﹣5x﹣9＝0 C、4x²+7x+9＝0 D、2x²﹣6x﹣10＝0

查看试题解析
6. 如图，平行四边形ABCD的对角线相交于点O，若AD⊥BD，AB＝10，BC＝6，则对角线AC的长是（）

A、4 $\sqrt{5}$ B、12 C、2 $\sqrt{13}$ D、4 $\sqrt{13}$

查看试题解析
7. 若反比例函数y＝﹣ $\frac{3}{x}$ 的图象上有3个点A（x₁ ， y₁），B（x₂ ， y₂），C（x₃ ， y₃），且满足x₁＜x₂＜0＜x₃ ，则y₁、y₂、y₃的大小关系是（）

A、y₃＜y₂＜y₁ B、y₃＜y₁＜y₂ C、y₁＜y₂＜y₃ D、y₂＜y₁＜y₃

查看试题解析
8. 用反证法证明命题“四边形中至少有一个角是钝角或直角”，应假设（）

A、四边形中所有角都是锐角 B、四边形中至多有一个角是钝角或直角 C、四边形中没有一个角是锐角 D、四边形中所有角都是钝角或直角

查看试题解析
9. 如图，平行四边形ABCD的一边AB∥y轴，顶点B在x轴上，顶点A，C在双曲线y₁＝ $\frac{k_{1}}{x}$ （k₁＞0，x＞0）上，顶点D在双曲线y₂＝ $\frac{k_{2}}{x}$ （k₂＞0，x＞0）上，其中点C的坐标为（3，1），当四边形ABCD的面积为 $\frac{9}{2}$ 时，k₂的值是（）

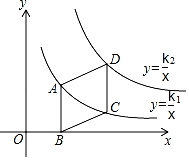A、7.5 B、9 C、10.5 D、21

查看试题解析
10. 如图，正方形ABCD中，点E，F，G，H分别是各边的中点，连结GH，取GH的中点P，连结EP，FP，则下列说法正确的是（）

A、PE＝ $\sqrt{2}$ GH B、四边形BEPF的周长是△GDH周长的3倍 C、∠EPF＝60° D、四边形BEPF的面积是△GDH面积的3倍

查看试题解析

二、填空题（每小题3分，共18分）

11. 化简： $\sqrt{4 \times 5}$ ＝.

查看试题解析
12. 一个多边形的内角和为900°，则这个多边形的边数为．

查看试题解析
13. 若m是方程2x²﹣x﹣1＝0的一个根，则代数式2m﹣4m²的值为.

查看试题解析
14. 某校学生的数学期末总评成绩由平时成绩、期中成绩、期末成绩3个部分组成，各部分比例如图所示.小明这三项的成绩依次是90分，85分，92分，则小明的期末总评成绩是.

查看试题解析
15. 如图，等腰△ABC中，AB＝AC＝6，∠BAC＝120°，点D，点P分别在AB，BC上运动，则线段AP和线段DP之和的最小值是.

查看试题解析
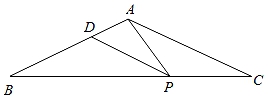16. 如图，直线y＝mx+n与双曲线y＝ $\frac{k}{x}$ （k＞0，x＞0）相交于点A（2，4），与y轴相交于点B（0，2），点C在该反比例函数的图象上运动，当△ABC的面积超过5时，点C的横坐标t的取值范围是.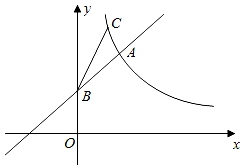

查看试题解析

三、解答题（第17～19题各6分，

17. 化简：

(1)、3 $\sqrt{3}$ ﹣（ $\sqrt{12}$ + $\sqrt{\frac{1}{3}}$ ）

(2)、（ $\sqrt{18}$ ﹣ $\sqrt{24}$ ）÷ $\sqrt{6}$ .

查看试题解析
18. 解方程：

(1)、（x﹣3）²﹣4＝0.

(2)、x²+5＝3（x+2）.

查看试题解析

19. 如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥，它用粗大的钢索将桥面拉住，为检测钢索的抗拉强度，桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测，数据统计如下（单位：百吨）

甲、乙两厂钢索抗拉强度检测统计表

钢索	1	2	3	4	5	平均数	中位数	方差
甲厂	10	11	9	10	12	10.4	10	1.04
乙厂	10	8	12	7	13	a	b	c

(1)、求乙厂5根钢索抗拉强度的平均数a（百吨）、中位数b（百吨）和方差c（平方百吨）.

(2)、桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量，问哪一家的钢索质量更优？

查看试题解析

20. 已知反比例函数的图象的一支如图所示，它经过点A（﹣4，2）.

(1)、求这个反比例函数的解析式；

(2)、补画这个反比例函数图象的另一支；

(3)、经过点A的直线y＝﹣2x+m与双曲线的另一个交点为B，连结OA，OB，求△AOB的面积.

查看试题解析
21. 如图，在矩形ABCD中，对角线BD的垂直平分线MN分别与AD、BC相交于点M、N，与BD相交于点O，连结BM，DN.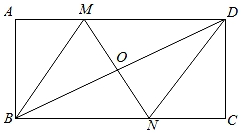

(1)、求证：四边形BMDN是菱形；

(2)、若MD＝2AM，BD＝8，求矩形ABCD的周长.

查看试题解析
22. 某一农家计划用篱笆围一个面积为12m²的矩形园子ABCD，其中AD边利用已有的一堵墙，其余三边用篱笆围起来.现已知墙的长为7.9m，可以选用的篱笆总长为11m.

(1)、若取矩形园子的边长都是整数米，问一共有哪些围法？

(2)、当矩形园子的边AB和BC分别是多长时，11m长的篱笆恰好用完？

查看试题解析
23. 如图1，凸四边形ABCD中，∠A＝90°，AB＝AD，若顶点B，C，D中存在某点到对角线的距离等于该对角线的一半，则称这个四边形为“距离和谐四边形”，这条对角线称为和谐对角线.如点C到对角线BD的距离是BD的一半，则四边形ABCD是距离和谐四边形，BD称为和谐对角线.显然，正方形ABCD属于距离和谐四边形，它的两条对角线都是和谐对角线.

(1)、如图2，在4×4的网格中，点A，B，D都是网格的格点，请你确定所有格点C，使得四边形ABCD是以BD为和谐对角线的距离和谐四边形；

(2)、如图1，距离和谐四边形ABCD中，∠A＝90°，AB＝AD＝3，
①若BD为和谐对角线，求线段AC的取值范围；

②若AC为和谐对角线，记AC的长度值为x，四边形ABCD的面积值为s，当s＝2x时，求x的值.

查看试题解析