四川省广元市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、-22. 下列运算正确的是( )A、 B、 C、 D、3. 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
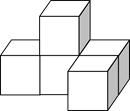 A、
A、 B、
B、 C、
C、 D、
D、 4. 在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
4. 在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:成绩(m)
1.80
1.50
1.60
1.65
1.70
1.75
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是( )
A、 B、 C、 D、5. 如图,a∥b,M、N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( ).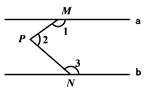 A、180° B、360° C、270° D、540°6. 按照如图所示的流程,若输出的 ,则输入的m为( )
A、180° B、360° C、270° D、540°6. 按照如图所示的流程,若输出的 ,则输入的m为( )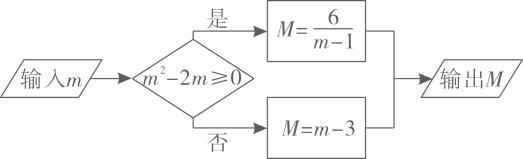 A、3 B、1 C、0 D、-17. 下列各图是截止2020年6月18日的新冠肺疫情统计数据,则以下结论错误的是( )图1 海外疫情
A、3 B、1 C、0 D、-17. 下列各图是截止2020年6月18日的新冠肺疫情统计数据,则以下结论错误的是( )图1 海外疫情地区 新增确诊 累计确诊 治煎 死亡 每百万人确诊 美国 26071 2234471 918796 119941 67917052 巴西 32188 955377 521046 46510 44853380 俄罗斯 7730 560279 313387 7638 38908264 印度 12881 366946 194325 12237 2659029 英国 1117 300717 1304 42238 44883134 西班牙 355 291763 196958 27136 62077234 秘鲁 3752 240908 128622 7257 73002424 意大利 328 237828 179455 34448 39638000 智利 36179 220628 181931 3615 116120000 伊朗 2596 197647 156991 9272 23529405 法国 458 194805 73791 29578 29075373 
 A、图1显示印度新增确诊人数大约是伊朗的两倍.每百万人口的确诊人数大约是伊朗的 B、图1显示俄罗斯当前的治愈率高于四班牙 C、图2显示海外新增确诊人数随时间的推移总体呈增长趋势 D、图3显示在2-3月之间,我国现有确诊人数达到最多8. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、9. 如图, 是 的两条互相垂直的直径,点P从点O出发,沿 的路线匀速运动,设 (单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )
A、图1显示印度新增确诊人数大约是伊朗的两倍.每百万人口的确诊人数大约是伊朗的 B、图1显示俄罗斯当前的治愈率高于四班牙 C、图2显示海外新增确诊人数随时间的推移总体呈增长趋势 D、图3显示在2-3月之间,我国现有确诊人数达到最多8. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、9. 如图, 是 的两条互相垂直的直径,点P从点O出发,沿 的路线匀速运动,设 (单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )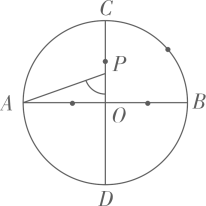 A、
A、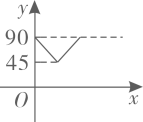 B、
B、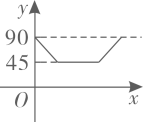 C、
C、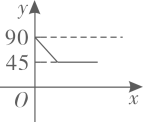 D、
D、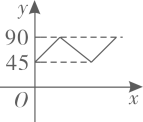 10. 规定: 给出以下四个结论:(1) ;(2) ;(3) ;(4) 其中正确的结论的个数为( )A、1个 B、2个 C、3个 D、4个
10. 规定: 给出以下四个结论:(1) ;(2) ;(3) ;(4) 其中正确的结论的个数为( )A、1个 B、2个 C、3个 D、4个二、填空题
-
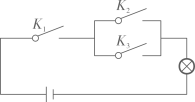
11. 近年来,四川省加快推进商业贸易转型升级,2019年,四川全省商业贸易服务业增加值达4194亿元,用科学记数法表示元.12. 在如图所示的电路图中,当随机闭合开关 , , 中的两个时,能够让灯泡发光的概率为 .
 13. 关于x的分式方程 的解为正数,则m的取值范围是 .14. 如图, 内接于 于点H,若 , 的半径为7,则 .
13. 关于x的分式方程 的解为正数,则m的取值范围是 .14. 如图, 内接于 于点H,若 , 的半径为7,则 .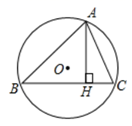 15. 如图所示, 均为等边三角形,边长分别为 ,B、C、D三点在同一条直线上,则下列结论正确的 . (填序号)
15. 如图所示, 均为等边三角形,边长分别为 ,B、C、D三点在同一条直线上,则下列结论正确的 . (填序号)① ② ③ 为等边三角形 ④ ⑤CM平分

三、解答题
-
16. 计算:17. 先化简,再求值: ,其中a是关于x的方程 的根.18. 已知 ,O为对角线AC的中点,过O的一条直线交AD于点E , 交BC于点F .
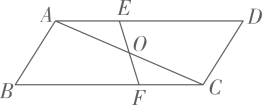 (1)、求证: ;(2)、若 , 的面积为2,求 的面积.19. 广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
(1)、求证: ;(2)、若 , 的面积为2,求 的面积.19. 广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题: (1)、求九年级(1)班共有多少名同学?(2)、补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;(3)、成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.20. 某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
(1)、求九年级(1)班共有多少名同学?(2)、补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;(3)、成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.20. 某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系: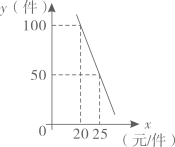 (1)、请求出y与x之间的函数关系式;(2)、该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;(3)、由于武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出300元捐赠给武汉,为了保证捐款后每天剩余利润不低于450元,如何确定该款电子产品的销售单价?21. 如图,公路MN为东西走向,在点M北偏东36.5°方向上,距离5千米处是学校A;在点M北偏东45°方向上距离 千米处是学校B.(参考数据: , ).
(1)、请求出y与x之间的函数关系式;(2)、该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;(3)、由于武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出300元捐赠给武汉,为了保证捐款后每天剩余利润不低于450元,如何确定该款电子产品的销售单价?21. 如图,公路MN为东西走向,在点M北偏东36.5°方向上,距离5千米处是学校A;在点M北偏东45°方向上距离 千米处是学校B.(参考数据: , ). (1)、求学校A , B两点之间的距离(2)、要在公路MN旁修建一个体育馆C , 使得A , B两所学校到体育馆C的距离之和最短,求这个最短距离.22. 如图所示,一次函数 的图象与反比例函数 的图象交于 .
(1)、求学校A , B两点之间的距离(2)、要在公路MN旁修建一个体育馆C , 使得A , B两所学校到体育馆C的距离之和最短,求这个最短距离.22. 如图所示,一次函数 的图象与反比例函数 的图象交于 .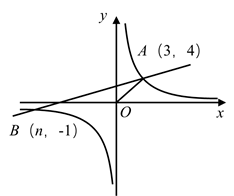 (1)、求反比例函数和一次函数的解析式;(2)、在x轴上存在一点C,使 为等腰三角形,求此时点C的坐标;(3)、根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
(1)、求反比例函数和一次函数的解析式;(2)、在x轴上存在一点C,使 为等腰三角形,求此时点C的坐标;(3)、根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.

