四川省甘孜州2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 气温由-5℃上升了4℃时的气温是( )A、-1℃ B、1℃ C、-9℃ D、9℃2. 如图摆放的下列几何体中,左视图是圆的是( )A、
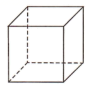 B、
B、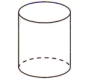 C、
C、 D、
D、 3. 月球与地球之间的平均距离约为38.4万公里,38.4万用科学记数法表示为( )A、 B、 C、 D、4. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、5. 在平面直角坐标系中,点 关于x轴对称的点是( )A、 B、 C、 D、6. 分式方程 的解为( )A、 B、 C、 D、7. 如图,菱形ABCD中,对角线AC , BD相交于点O , E为AB的中点.若菱形ABCD的周长为32,则OE的长为( )
3. 月球与地球之间的平均距离约为38.4万公里,38.4万用科学记数法表示为( )A、 B、 C、 D、4. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、5. 在平面直角坐标系中,点 关于x轴对称的点是( )A、 B、 C、 D、6. 分式方程 的解为( )A、 B、 C、 D、7. 如图,菱形ABCD中,对角线AC , BD相交于点O , E为AB的中点.若菱形ABCD的周长为32,则OE的长为( ) A、3 B、4 C、5 D、68. 下列运算中,正确的是( )A、 B、 C、 D、9. 如图,等腰△ 中,点D , E分别在腰AB , AC上,添加下列条件,不能判定 ≌ 的是( )
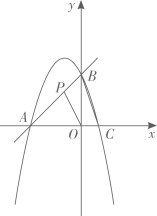
A、3 B、4 C、5 D、68. 下列运算中,正确的是( )A、 B、 C、 D、9. 如图,等腰△ 中,点D , E分别在腰AB , AC上,添加下列条件,不能判定 ≌ 的是( )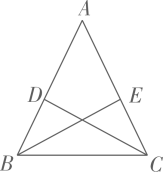 A、 B、 C、 D、10. 如图,二次函数 的图象与 轴交于 ,B两点,下列说法错误的是( )
A、 B、 C、 D、10. 如图,二次函数 的图象与 轴交于 ,B两点,下列说法错误的是( )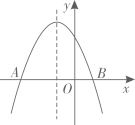 A、 B、图象的对称轴为直线 C、点B的坐标为 D、当 时,y随x的增大而增大
A、 B、图象的对称轴为直线 C、点B的坐标为 D、当 时,y随x的增大而增大二、填空题
-
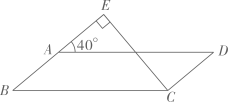
11. .12. 如图,在 中,过点C作 ,垂足为E , 若 ,则 的度数为 .
 13. 某班为了解同学们一周在校参加体育锻炼的时间,随机调查了10名同学,得到如下数据:
13. 某班为了解同学们一周在校参加体育锻炼的时间,随机调查了10名同学,得到如下数据:锻炼时闭(小时)
5
6
7
8
人数
1
4
3
2
则这10名同学一周在校参加体育锻炼时间的平均数是小时.
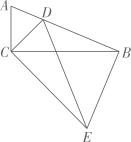
14. 如图,AB为 的直径,弦 于点H , 若 , ,则OH的长度为 .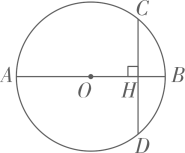 15. 在单词 (数学)中任意选择一个字母,选中字母“a”的概率为 .16. 若 ,则代数式 的值为 .17. 三角形的两边长分别为4和7,第三边的长是方程 的解,则这个三角形的周长是 .18. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
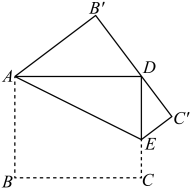
15. 在单词 (数学)中任意选择一个字母,选中字母“a”的概率为 .16. 若 ,则代数式 的值为 .17. 三角形的两边长分别为4和7,第三边的长是方程 的解,则这个三角形的周长是 .18. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
 19. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于A,B两点,若点P是第一象限内反比例函数图象上一点,且 的面积是 的面积的2倍,则点P的横坐标为 .
19. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于A,B两点,若点P是第一象限内反比例函数图象上一点,且 的面积是 的面积的2倍,则点P的横坐标为 .
三、解答题
-
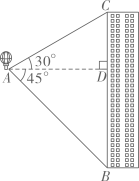
20.(1)、计算: .(2)、解不等式组:21. 化简: .22. 热气球的探测器显示,从热气球A处看大楼BC顶部C的仰角为30°,看大楼底部B的俯角为45°,热气球与该楼的水平距离AD为60米,求大楼BC的高度.(结果精确到1米,参考数据: )
 23. 如图,一次函数 的图象与反比例函数 的图象相交于 和B两点.
23. 如图,一次函数 的图象与反比例函数 的图象相交于 和B两点.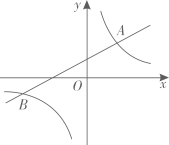 (1)、求反比例函数的解析式;(2)、求点B的坐标.24. 为了解同学们最喜欢一年四季中的哪个季节,数学社在全校随机抽取部分同学进行问卷调查,根据调查结果,得到如下两幅不完整的统计图.
(1)、求反比例函数的解析式;(2)、求点B的坐标.24. 为了解同学们最喜欢一年四季中的哪个季节,数学社在全校随机抽取部分同学进行问卷调查,根据调查结果,得到如下两幅不完整的统计图.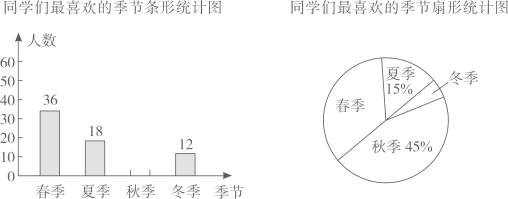
根据图中信息,解答下列问题:
(1)、此次调查一共随机抽取了名同学;扇形统计图中,“春季”所对应的扇形的圆心角的度数为;(2)、若该学校有1500名同学,请估计该校最喜欢冬季的同学的人数;(3)、现从最喜欢夏季的3名同学A,B,C中,随机选两名同学去参加学校组织的“我爱夏天”演讲比赛,请用列表或画树状图的方法求恰好选到A,B去参加比赛的概率.25. 如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.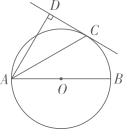 (1)、求证: ;(2)、若 , ,求CD的长.26. 某商品的进价为每件40元,在销售过程中发现,每周的销售量y(件)与销售单价x(元)之间的关系可以近似看作一次函数 ,且当售价定为50元/件时,每周销售30件,当售价定为70元/件时,每周销售10件.(1)、求k , b的值;(2)、求销售该商品每周的利润w(元)与销售单价x(元)之间的函数解析式,并求出销售该商品每周可获得的最大利润.
(1)、求证: ;(2)、若 , ,求CD的长.26. 某商品的进价为每件40元,在销售过程中发现,每周的销售量y(件)与销售单价x(元)之间的关系可以近似看作一次函数 ,且当售价定为50元/件时,每周销售30件,当售价定为70元/件时,每周销售10件.(1)、求k , b的值;(2)、求销售该商品每周的利润w(元)与销售单价x(元)之间的函数解析式,并求出销售该商品每周可获得的最大利润.