四川省达州市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 人类与病毒的斗争是长期的,不能松懈.据中央电视台“朝日新闻”报道,截止北京时间2020年6月30日凌晨,全球新冠肺炎患者确诊病例达到1002万.1002万用科学记数法表示,正确的是( )A、 B、 C、 D、 万2. 下列各数中,比3大比4小的无理数是( )A、3.14 B、 C、 D、3. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、
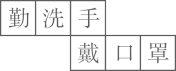 B、
B、 C、
C、 D、
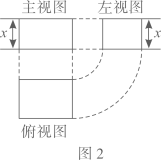
D、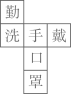 4. 下列说法正确的是( )A、为了解全国中小学生的心理健康状况,应采用普查. B、确定事件一定会发生. C、某校6位同学在新冠肺炎防疫知识竞赛中成绩分别为98、97、99、99、98、96,那么这组数据的众数为98. D、数据6、5、8、7、2的中位数是6.5. 图2是图1中长方体的三视图,若用S表示面积, , ,则 ( )
4. 下列说法正确的是( )A、为了解全国中小学生的心理健康状况,应采用普查. B、确定事件一定会发生. C、某校6位同学在新冠肺炎防疫知识竞赛中成绩分别为98、97、99、99、98、96,那么这组数据的众数为98. D、数据6、5、8、7、2的中位数是6.5. 图2是图1中长方体的三视图,若用S表示面积, , ,则 ( )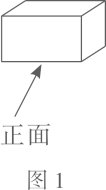
 A、 B、 C、 D、6. 如图,正方体的每条棱上放置相同数目的小球,设每条棱上的小球数为m,下列代数式表示正方体上小球总数,则表达错误的是( )
A、 B、 C、 D、6. 如图,正方体的每条棱上放置相同数目的小球,设每条棱上的小球数为m,下列代数式表示正方体上小球总数,则表达错误的是( )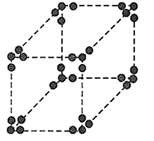 A、 B、 C、 D、7. 中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )
A、 B、 C、 D、7. 中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )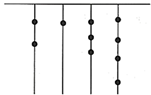 A、10 B、89 C、165 D、2948. 如图,在半径为5的 中,将劣弧 沿弦 翻折,使折叠后的 恰好与 、 相切,则劣弧AB的长为( )
A、10 B、89 C、165 D、2948. 如图,在半径为5的 中,将劣弧 沿弦 翻折,使折叠后的 恰好与 、 相切,则劣弧AB的长为( )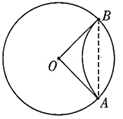 A、 B、 C、 D、9. 如图,直线 与抛物线 交于A、B两点,则 的图象可能是( )
A、 B、 C、 D、9. 如图,直线 与抛物线 交于A、B两点,则 的图象可能是( )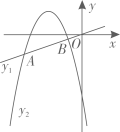 A、
A、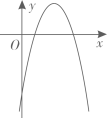 B、
B、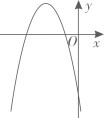 C、
C、 D、
D、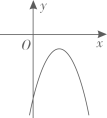 10. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( )
10. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 2019年是中华人民共和国成立70周年,天安门广场举行了盛大的国庆阅兵式和群众游行活动.其中,群众游行队伍以“同心共筑中国梦”为主题,包含有“建国创业”“改革开放”“伟大复兴”三个部分,某同学要统计本班学生最喜欢哪个部分,制作扇形统计图.以下是打乱了的统计步骤:
①绘制扇形统计图
②收集三个部分本班学生喜欢的人数
③计算扇形统计图中三个部分所占的百分比
其中正确的统计顺序是 .
12. 如图,点 与点 关于直线 对称,则 . 13. 小明为测量校园里一颗大树 的高度,在树底部B所在的水平面内,将测角仪 竖直放在与B相距 的位置,在D处测得树顶A的仰角为 .若测角仪的高度是 ,则大树 的高度约为 . (结果精确到 .参考数据: )
13. 小明为测量校园里一颗大树 的高度,在树底部B所在的水平面内,将测角仪 竖直放在与B相距 的位置,在D处测得树顶A的仰角为 .若测角仪的高度是 ,则大树 的高度约为 . (结果精确到 .参考数据: ) 14. 如图,点A、B在反比函数 的图象上,A、B的纵坐标分别是3和6,连接 、 ,则 的面积是 .
14. 如图,点A、B在反比函数 的图象上,A、B的纵坐标分别是3和6,连接 、 ,则 的面积是 . 15. 已知 的三边a、b、c满足 ,则 的内切圆半径= .16. 已知k为正整数,无论k取何值,直线 与直线 都交于一个固定的点,这个点的坐标是;记直线 和 与x轴围成的三角形面积为 ,则 , 的值为 .
15. 已知 的三边a、b、c满足 ,则 的内切圆半径= .16. 已知k为正整数,无论k取何值,直线 与直线 都交于一个固定的点,这个点的坐标是;记直线 和 与x轴围成的三角形面积为 ,则 , 的值为 .三、解答题
-
17. 计算: .18. 求代数式 的值,其中 .19. 如图,点O在 的边 上,以 为半径作 , 的平分线 交 于点D,过点D作 于点E.
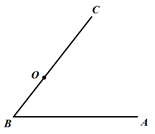 (1)、尺规作图(不写作法,保留作图痕迹),补全图形;(2)、判断 与 交点的个数,并说明理由.20. 争创全国文明城市,从我做起.尚理中学在八年级开设了文明礼仪校本课程,为了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:
(1)、尺规作图(不写作法,保留作图痕迹),补全图形;(2)、判断 与 交点的个数,并说明理由.20. 争创全国文明城市,从我做起.尚理中学在八年级开设了文明礼仪校本课程,为了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:94 83 90 86 94 88 96 100 89 82
94 82 84 89 88 93 98 94 93 92
整理上面的数据,得到频数分布表和扇形统计图:
等级
成绩/分
频数
A
a
B
8
C
5
D
4
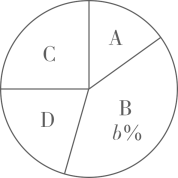
根据以上信息,解答下列问题.
(1)、填空: , ;(2)、若成绩不低于90分为优秀,估计该校1200名八年级学生中,达到优秀等级的人数;(3)、已知A等级中有2名女生,现从A等级中随机抽取2名同学,试用列表或画树状图的方法求出恰好抽到一男一女的概率.21. 如图, 中, ,D、E分别是边 、 的中点.将 绕点E旋转180度,得 .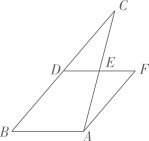 (1)、判断四边形 的形状,并证明;(2)、已知 , ,求四边形 的面积S.22. 某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
(1)、判断四边形 的形状,并证明;(2)、已知 , ,求四边形 的面积S.22. 某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
380
940
餐椅
160
已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同.
(1)、求表中a的值;(2)、该商场计划购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.若将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售,请问怎样进货,才能获得最大利润?最大利润是多少?23. 如图,在梯形 中, , , , .P为线段 上的一动点,且和B、C不重合,连接 ,过点P作 交射线 于点E.聪聪根据学习函数的经验,对这个问题进行了研究:
 (1)、通过推理,他发现 ,请你帮他完成证明.(2)、利用几何画板,他改变 的长度,运动点P,得到不同位置时, 、 的长度的对应值:
(1)、通过推理,他发现 ,请你帮他完成证明.(2)、利用几何画板,他改变 的长度,运动点P,得到不同位置时, 、 的长度的对应值:当 时,得表1:
…
1
2
3
4
5
…
…
0.83
1.33
1.50
1.33
0.83
…
当 时,得表2:
…
1
2
3
4
5
6
7
…
…
1.17
2.00
2.50
2.67
2.50
2.00
1.17
…
这说明,点P在线段 上运动时,要保证点E总在线段 上, 的长度应有一定的限制.
①填空:根据函数的定义,我们可以确定,在 和 的长度这两个变量中,的长度为自变量,的长度为因变量;
②设 ,当点P在线段 上运动时,点E总在线段 上,求m的取值范围.
24.(1)、(阅读与证明)如图1,在正 的外角 内引射线 ,作点C关于 的对称点E(点E在 内),连接 , 、 分别交 于点F、G.

①完成证明: 点E是点C关于 的对称点,
, , .
正 中, , ,
,得 .
在 中, , .
在 中, , .
②求证: .
(2)、(类比与探究)把(1)中的“正 ”改为“正方形 ”,其余条件不变,如图2.类比探究,可得:
① ;
②线段 、 、 之间存在数量关系 .
 (3)、(归纳与拓展)
(3)、(归纳与拓展)如图3,点A在射线 上, , ,在 内引射线 ,作点C关于 的对称点E(点E在 内),连接 , 、 分别交 于点F、G.则线段 、 、 之间的数量关系为 .
 25. 如图,在平面直角坐标系 xOy 中,已知直线 与x轴交于点A,与y轴交于点B,过A、B两点的抛物线 与x轴交于另一点 .
25. 如图,在平面直角坐标系 xOy 中,已知直线 与x轴交于点A,与y轴交于点B,过A、B两点的抛物线 与x轴交于另一点 . (1)、求抛物线的解析式;(2)、在抛物线上是否存在一点P,使 ?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、点M为直线 下方抛物线上一点,点N为y轴上一点,当 的面积最大时,求 的最小值.
(1)、求抛物线的解析式;(2)、在抛物线上是否存在一点P,使 ?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、点M为直线 下方抛物线上一点,点N为y轴上一点,当 的面积最大时,求 的最小值.