江苏省扬州市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、选择题
-
1. 实数3的相反数是( )A、-3 B、 C、3 D、±32. 下列各式中,计算结果为 的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. “致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光.在下列与扬州有关的标识或简图中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:
5. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:调查问卷 ________年________月________日
你平时最喜欢的一种体育运动项目是( )(单选)
A. B. C. D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是( )
A、①②③ B、①③⑤ C、②③④ D、②④⑤6. 如图,小明从点A出发沿直线前进10米到达点B,向左转 后又沿直线前进10米到达点C,再向左转 后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
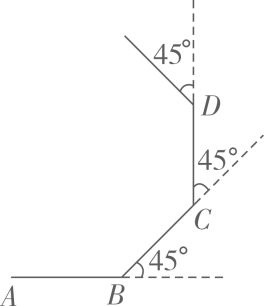 A、100米 B、80米 C、60米 D、40米7. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
A、100米 B、80米 C、60米 D、40米7. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
 A、 B、 C、 D、8. 小明同学利用计算机软件绘制函数 (a、b为常数)的图像如图所示,由学习函数的经验,可以推断常数a、b的值满足( )
A、 B、 C、 D、8. 小明同学利用计算机软件绘制函数 (a、b为常数)的图像如图所示,由学习函数的经验,可以推断常数a、b的值满足( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题
-
9. 2020年6月23日,中国自主研发的北斗三号最后一颗卫星成功发射.据统计,国内已有超过6500000辆营运车辆导航设施应用北斗系统,数据6500000用科学记数法表示为.10. 分解因式: .11. 代数式 在实数范围内有意义,则实数x的取值范围是.12. 方程(x+1)2=9的解是.13. 圆锥的底面半径为3,侧面积为 ,则这个圆锥的母线长为.14. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高.
 15. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
15. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 . 16. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 cm.
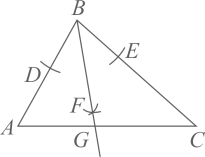
16. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 cm.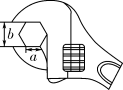 17. 如图,在 中,按以下步骤作图:
17. 如图,在 中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交AB、BC于点D、E.
②分别以点D、E为圆心,大于 的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果 , , 的面积为18,则 的面积为.
 18. 如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为.
18. 如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为.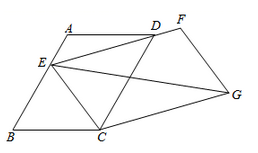
三、解答题
-
19. 计算或化简:(1)、(2)、20. 解不等式组 ,并写出它的最大负整数解.21. 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.

根据以上信息,回答下列问题:
(1)、本次调查的样本容量是 , 扇形统计图中表示A等级的扇形圆心角为 ;(2)、补全条形统计图;(3)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.22. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.23. 如图,某公司会计欲查询乙商品的进价,发现进货单已被墨水污染.进货单
商品
进价(元/件)
数量(件)
总金额(元)
甲

7200
乙
3200
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下:
李阿姨:我记得甲商品进价比乙商品进价每件高50%.
王师傅:甲商品比乙商品的数量多40件.
请你求出乙商品的进价,并帮助他们补全进货单.
24. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE. (1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.25. 如图, 内接于 , ,点E在直径CD的延长线上,且 .
(1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.25. 如图, 内接于 , ,点E在直径CD的延长线上,且 .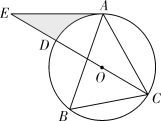 (1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.26. 阅读感悟:
(1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.26. 阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数x、y满足 ①, ②,求 和 的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由① ②可得 ,由① ② 可得 .这样的解题思想就是通常所说的“整体思想”.
解决问题:
(1)、已知二元一次方程组 ,则 , ;(2)、某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?(3)、对于实数x、y,定义新运算: ,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知 , ,那么 .27. 如图1,已知点O在四边形ABCD的边AB上,且 ,OC平分 ,与BD交于点G,AC分别与BD、OD交于点E、F.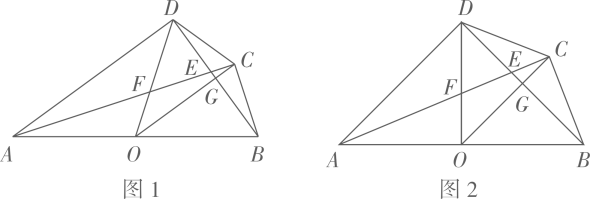 (1)、求证: ;(2)、如图2,若 ,求 的值;(3)、当四边形ABCD的周长取最大值时,求 的值.28. 如图,已知点 、 ,点P为线段AB上的一个动点,反比例函数 的图像经过点P.小明说:“点P从点A运动至点B的过程中,k值逐渐增大,当点P在点A位置时k值最小,在点B位置时k值最大.”
(1)、求证: ;(2)、如图2,若 ,求 的值;(3)、当四边形ABCD的周长取最大值时,求 的值.28. 如图,已知点 、 ,点P为线段AB上的一个动点,反比例函数 的图像经过点P.小明说:“点P从点A运动至点B的过程中,k值逐渐增大,当点P在点A位置时k值最小,在点B位置时k值最大.”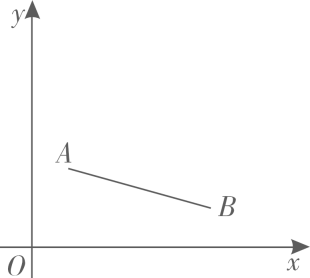 (1)、当 时.
(1)、当 时.①求线段AB所在直线的函数表达式.
②你完全同意小明的说法吗?若完全同意,请说明理由;若不完全同意,也请说明理由,并求出正确的k的最小值和最大值.
(2)、若小明的说法完全正确,求n的取值范围.