江苏省无锡市2020年中考数学试卷

试卷更新日期：2020-07-28 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣7的倒数是（　　）

A、 $\frac{1}{7}$ B、7 C、- $\frac{1}{7}$ D、﹣7

查看试题解析
2. 函数 $y = 2 + \sqrt{3 x - 1}$ 中自变量 $x$ 的取值范围是（）

A、 $x \geq 2$ B、 $x \geq \frac{1}{3}$ C、 $x \leq \frac{1}{3}$ D、 $x \neq \frac{1}{3}$

查看试题解析
3. 已知一组数据：21，23，25，25，26，这组数据的平均数和中位数分别是（）

A、24，25 B、24，24 C、25，24 D、25，25

查看试题解析
4. 若 $x + y = 2$ ， $z - y = - 3$ ，则 $x + z$ 的值等于（）

A、5 B、1 C、-1 D、-5

查看试题解析
5. 正十边形的每一个外角的度数为（）

A、 $36 °$ B、 $30 °$ C、 $144 °$ D、 $150 °$

查看试题解析
6. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、圆 B、等腰三角形 C、平行四边形 D、菱形

查看试题解析
7. 下列选项错误的是（）

A、 $\cos 60 ° = \frac{1}{2}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 $\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ D、 $2 (x - 2 y) = 2 x - 2 y$

查看试题解析
8. 反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = \frac{8}{15} x + \frac{16}{15}$ 的图形有一个交点 $B (\frac{1}{2} ， m)$ ，则k的值为（）

A、1 B、2 C、 $\frac{2}{3}$ D、 $\frac{4}{3}$

查看试题解析
9. 如图，在四边形 $A B C D$ 中 $(A B > C D)$ ， $∠ A B C = ∠ B C D = 90 °$ ， $A B = 3$ ， $B C = \sqrt{3}$ ，把 $R t Δ A B C$ 沿着 $A C$ 翻折得到 $R t Δ A E C$ ，若 $\tan ∠ A E D = \frac{\sqrt{3}}{2}$ ，则线段 $D E$ 的长度为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{7}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{2 \sqrt{7}}{5}$

查看试题解析
10. 如图，等边 $Δ A B C$ 的边长为3，点D在边 $A C$ 上， $A D = \frac{1}{2}$ ，线段 $P Q$ 在边 $B A$ 上运动， $P Q = \frac{1}{2}$ ，有下列结论：

① $C P$ 与 $Q D$ 可能相等；② $Δ A Q D$ 与 $Δ B C P$ 可能相似；③四边形 $P C D Q$ 面积的最大值为 $\frac{31 \sqrt{3}}{16}$ ；④四边形 $P C D Q$ 周长的最小值为 $3 + \frac{\sqrt{37}}{2}$ .其中，正确结论的序号为（）

A、①④ B、②④ C、①③ D、②③

查看试题解析

二、填空题

11. 因式分解： $a b^{2} - 2 a b + a =$ .

查看试题解析
12. 2019年我市地区生产总值逼近12000亿元，用科学记数法表示12000 是.

查看试题解析
13. 已知圆锥的底面半径为 $1 c m$ ，高为 $\sqrt{3} c m$ ，则它的侧面展开图的面积为=.

查看试题解析
14. 如图，在菱形 $A B C D$ 中， $∠ B = 50 °$ ，点E在 $C D$ 上，若 $A E = A C$ ，则 $∠ B A E =$ .

查看试题解析
15. 请写出一个函数表达式，使其图象的对称轴为 $y$ 轴：.

查看试题解析
16. 我国古代问题：以绳测井，若将绳三折测之，绳多四尺，若将绳四折测之，绳多一尺，井深几何？这段话的意思是：用绳子最井深，把绳三折来量，井外余绳四尺，把绳四折来量，井外余绳一尺，井深几尺？则该问题的井深是尺.

查看试题解析
17. 二次函数 $y = a x^{2} - 3 a x + 3$ 的图像过点 $A (6 ， 0)$ ，且与y轴交于点B，点M在该抛物线的对称轴上，若 $Δ A B M$ 是以 $A B$ 为直角边的直角三角形，则点M的坐标为.

查看试题解析
18. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 4$ ，点D，E分别在边 $A B$ ， $A C$ 上，且 $D B = 2 A D$ ， $A E = 3 E C$ 连接 $B E$ ， $C D$ ，相交于点O，则 $Δ A B O$ 面积最大值为.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 2)}^{2} + | - 5 | - \sqrt{16}$

(2)、 $\frac{a - 1}{a - b} - \frac{1 + b}{b - a}$ .

查看试题解析
20. 解方程：

(1)、 $x^{2} + x - 1 = 0$

(2)、 ${\begin{array}{l} - 2 x \leq 0 \\ 4 x + 1 < 5 \end{array}$

查看试题解析
21. 如图，已知 $A B / / C D$ ， $A B = C D$ ， $B E = C F$ .

求证：

(1)、 $Δ A B F ≅ Δ D C E$ ；

(2)、 $A F / / D E$ .

查看试题解析
22. 现有4张正面分别写有数字1、2、3、4的卡片，将4张卡片的背面朝上，洗匀.

(1)、若从中任意抽取1张，抽的卡片上的数字恰好为3的概率是；

(2)、若先从中任意抽取1张（不放回），再从余下的3张中任意抽取1张，求抽得的2张卡片上的数字之和为3的倍数的概率.（请用“画树状图”或“列表”等方法写出分析过程）

查看试题解析

23. 小李2014年参加工作，每年年底都把本年度收入减去支出后的余额存入银行（存款利息记入收入），2014年底到2019年底，小李的银行存款余额变化情况如下表所示：（单位：万元）

年份	2014年	2015年	2016年	2017年	2018年	2019年
收入	3	8	9	a	14	18
支出	1	4	5	6	c	6
存款余额	2	6	10	15	b	34

(1)、表格中

a =

；

(2)、请把下面的条形统计图补充完整：（画图后标注相应的数据）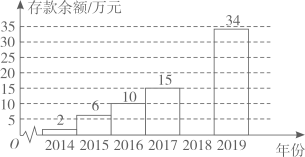

(3)、请问小李在哪一年的支出最多？支出了多少万元？

查看试题解析

24. 如图，已知 $Δ A B C$ 是锐角三角形 $(A C < A B)$ .

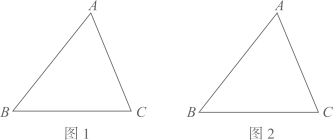(1)、请在图1中用无刻度的直尺和圆规作图；作直线l，使l上的各点到B、C两点的距离相等；设直线 $l$ 与 $A B$ 、 $B C$ 分别交于点M、N，作一个圆，使得圆心O在线段 $M N$ 上，且与边 $A B$ 、 $B C$ 相切；（不写作法，保留作图痕迹）

(2)、在（1）的条件下，若 $B M = \frac{5}{3}$ ， $B C = 2$ ，则 $⊙ O$ 的半径为.

查看试题解析
25. 如图， $D B$ 过 $⊙ O$ 的圆心，交 $⊙ O$ 于点A、B， $D C$ 是 $⊙ O$ 的切线，点C是切点，已知 $∠ D = 30 °$ ， $D C = \sqrt{3}$ .

(1)、求证： $Δ B O C \sim Δ B C D$ ；

(2)、求 $Δ B C D$ 的周长.

查看试题解析
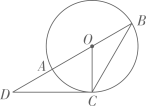26. 有一块矩形地块 $A B C D$ ， $A B = 20$ 米， $B C = 30$ 米，为美观，拟种植不同的花卉，如图所示，将矩形 $A B C D$ 分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x米.现决定在等腰梯形 $A E H D$ 和 $B C G F$ 中种植甲种花卉；在等腰梯形 $A B F E$ 和 $C D H G$ 中种植乙种花卉；在矩形 $E F G H$ 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米 $^{2}$ 、60 元/米 $^{2}$ 、40元/米 $^{2}$ ，设三种花卉的种植总成本为y元.

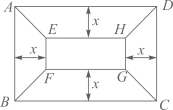(1)、当 $x = 5$ 时，求种植总成本y；

(2)、求种植总成本y与x的函数表达式，并写出自变量x的取值范围；

(3)、若甲、乙两种花卉的种植面积之差不超过120米 $^{2}$ ，求三种花卉的最低种植总成本.

查看试题解析
27. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $A D = 1$ ，点E为边 $C D$ 上的一点（与C、D不重合）四边形 $A B C E$ 关于直线 $A E$ 的对称图形为四边形 $A N M E$ ，延长 $M E$ 交 $A B$ 与点P，记四边形 $P A D E$ 的面积为S.

(1)、若 $D E = \frac{\sqrt{3}}{3}$ ，求S的值；

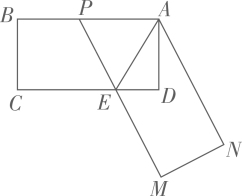(2)、设 $D E = x$ ，求S关于x的函数表达式.

查看试题解析
28. 在平面直角坐标系中，O为坐标原点，直线 $O A$ 交二次函数 $y = \frac{1}{4} x^{2}$ 的图像于点A， $∠ A O B = 90 °$ ，点 $B$ 在该二次函数的图象上，设过点 $(0 ， m)$ （其中 $m > 0$ ）且平行于 $x$ 轴的直线交直线 $O A$ 于点M，交直线 $O B$ 于点N，以线段 $O M$ 、 $O N$ 为邻边作矩形 $O M P N$ .

(1)、若点A的横坐标为8.
①用含m的代数式表示M的坐标；

②点 $P$ 能否落在该二次函数的图象上？若能，求出m的值；若不能，请说明理由；

(2)、当 $m = 2$ 时，若点 $P$ 恰好落在该二次函数的图象上，请直接写出此时满足条件的所有直线 $O A$ 的函数表达式.

查看试题解析