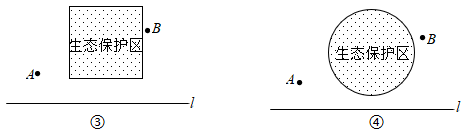江苏省南京市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、选择题
-
1. 计算 的结果是( )A、-5 B、-1 C、1 D、52. 3的平方根是( )A、 9 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据, 年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法错误的是( )
 A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务5. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根6. 如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )
A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务5. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根6. 如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )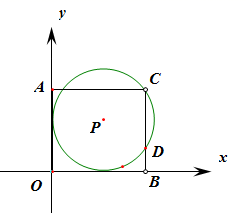 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
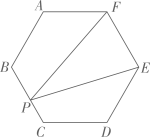
7. 写出一个负数,使这个数的绝对值小于3.8. 若式子 在实数范围内有意义,则x的取值范围是.9. 纳秒 是非常小的时间单位, ,北斗全球导航系统的授时精度优于 ,用科学记数法表示 是.10. 计算 的结果是.11. 已知x、y满足方程组 ,则 的值为.12. 方程 的解是.13. 将一次函数 的图象绕原点O逆时针旋转 ,所得到的图像对应的函数表达式是.14. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.
 15. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 =.
15. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 =.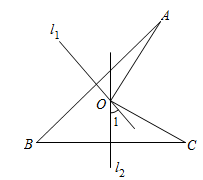 16. 下列关于二次函数 ( 为常数)的结论,①该函数的图象与函数 的图象形状相同;②该函数的图象一定经过点 ;③当 时,y随x的增大而减小;④该函数的图象的顶点在函数 的图像上,其中所有正确的结论序号是.
16. 下列关于二次函数 ( 为常数)的结论,①该函数的图象与函数 的图象形状相同;②该函数的图象一定经过点 ;③当 时,y随x的增大而减小;④该函数的图象的顶点在函数 的图像上,其中所有正确的结论序号是.三、解答题
-
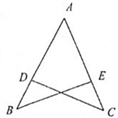
17. 计算:18. 解方程: .19. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BD=CE.
 20. 已知反比例函数 的图象经过点(1)、求k的值(2)、完成下面的解答
20. 已知反比例函数 的图象经过点(1)、求k的值(2)、完成下面的解答解不等式组
解:解不等式①,得.
根据函数 的图象,得不等式②得解集.
把不等式①和②的解集在数轴上表示出来

从中可以找出两个不等式解集的公共部分,得不等式组的解集.
21. 为了了解某地居民的用电量情况,随机抽取了该地200户居民六月份的用电量(单位: )进行调查,整理样本数据得到下面的频数分布表:组别
用电量分组
频数
1
50
2
100
3
34
4
11
5
1
6
1
7
2
8
1
根据抽样调查的结果,回答下列问题:
(1)、该地这200户居民六月份的用电量的中位数落在第组内.(2)、估计该地1万户居民六月份的用电量低于 的大约有多少户.22. 甲、乙两人分别从A、B、C这3个景点随机选择2个景点游览.(1)、求甲选择的2个景点是A、B的概率.(2)、甲、乙两人选择的2个景点恰好相同的概率是.23. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )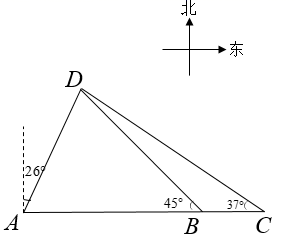 24. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证:
24. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证: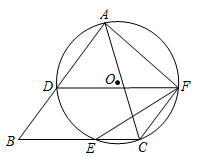 (1)、四边形DBCF是平行四边形(2)、25. 小明和小丽先后从A地出发同一直道去B地, 设小丽出发第 时, 小丽、小明离B地的距离分别为 、 , 与x之间的数表达式 , 与x之间的函数表达式是 .(1)、小丽出发时,小明离A地的距离为 .(2)、小丽发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?26. 如图,在 和 中,D、 分别是AB、 上一点, .
(1)、四边形DBCF是平行四边形(2)、25. 小明和小丽先后从A地出发同一直道去B地, 设小丽出发第 时, 小丽、小明离B地的距离分别为 、 , 与x之间的数表达式 , 与x之间的函数表达式是 .(1)、小丽出发时,小明离A地的距离为 .(2)、小丽发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?26. 如图,在 和 中,D、 分别是AB、 上一点, .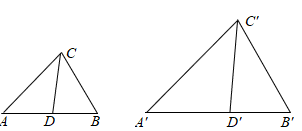 (1)、当 时,求证: 证明的途径可以用如框图表示,请填写其中的空格
(1)、当 时,求证: 证明的途径可以用如框图表示,请填写其中的空格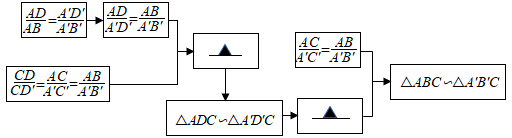 (2)、当 时,判断 与 是否相似,并说明理由27. 如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短.
(2)、当 时,判断 与 是否相似,并说明理由27. 如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短. (1)、如图②,作出点A关于l的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点 ,连接 , , 证明 , 请完成这个证明.
(1)、如图②,作出点A关于l的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点 ,连接 , , 证明 , 请完成这个证明.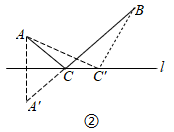 (2)、如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由),
(2)、如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由),①生市保护区是正方形区城,位置如图③所示
②生态保护区是圆形区域,位置如图④所示.