江苏省连云港市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、选择题
-
1. 3的绝对值是( ).A、 -3 B、3 C、 D、2. 下图是由4个大小相同的正方体搭成的几何体,这个几何体的主视图是( ).
 A、
A、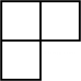 B、
B、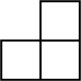 C、
C、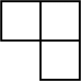 D、
D、 3. 下列计算正确的是( ).A、 B、 C、 D、4. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差5. 不等式组 的解集在数轴上表示为( ).A、
3. 下列计算正确的是( ).A、 B、 C、 D、4. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差5. 不等式组 的解集在数轴上表示为( ).A、 B、
B、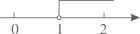 C、
C、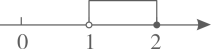 D、
D、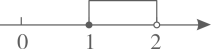 6. 如图,将矩形纸片 沿 折叠,使点A落在对角线 上的 处.若 ,则 等于( ).
6. 如图,将矩形纸片 沿 折叠,使点A落在对角线 上的 处.若 ,则 等于( ).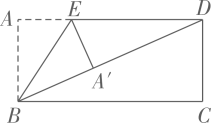 A、 B、 C、 D、7. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:
A、 B、 C、 D、7. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:①快车途中停留了 ;②快车速度比慢车速度多 ;③图中 ;④快车先到达目的地.其中正确的是( )
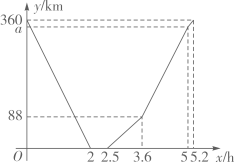 A、①③ B、②③ C、②④ D、①④
A、①③ B、②③ C、②④ D、①④二、填空题
-
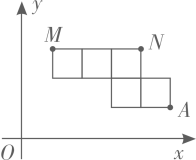
8. 我市某天的最高气温是4℃,最低气温是 ,则这天的日温差是℃.9. “我的连云港” 是全市统一的城市综合移动应用服务端.一年来,实名注册用户超过1600000人.数据“1600000”用科学记数法表示为.10. 如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为.
 11. 按照如图所示的计算程序,若 ,则输出的结果是.
11. 按照如图所示的计算程序,若 ,则输出的结果是.
 12. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位: )满足函数表达式 ,则最佳加工时间为 .13. 用一个圆心角为 ,半径为 的扇形纸片围成一个圆锥的侧面,这个圆锥的底面圆半径为 .14. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
12. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位: )满足函数表达式 ,则最佳加工时间为 .13. 用一个圆心角为 ,半径为 的扇形纸片围成一个圆锥的侧面,这个圆锥的底面圆半径为 .14. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .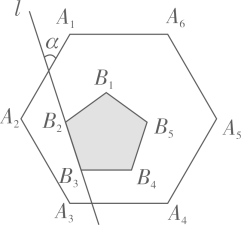 15. 如图,在平面直角坐标系 中,半径为2的 与 轴的正半轴交于点A,点B是 上一动点,点C为弦 的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为.
15. 如图,在平面直角坐标系 中,半径为2的 与 轴的正半轴交于点A,点B是 上一动点,点C为弦 的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为.
三、解答题
-
16. 计算 .17. 解方程组 .18. 化简 .19. 在世界环境日(6月5日),学校组织了保护环境知识测试,现从中随机抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”四个等级进行统计,绘制了如下尚不完整的统计图表.
测试成绩统计表
等级
频数(人数)
频率
优秀
30
良好
0.45
合格
24
0.20
不合格
12
0.10
合计
1

根据统计图表提供的信息,解答下列问题:
(1)、表中 , , ;(2)、补全条形统计图;(3)、若该校有2400名学生参加了本次测试,估计测试成绩等级在良好以上(包括良好)的学生约有多少人?20. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.21. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于M、N.
 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.22. 甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100000元,公司共捐款140000元.下面是甲、乙两公司员工的一段对话:
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.22. 甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100000元,公司共捐款140000元.下面是甲、乙两公司员工的一段对话:
 (1)、甲、乙两公司各有多少人?(2)、现甲、乙两公司共同使用这笔捐款购买A、B两种防疫物资,A种防疫物资每箱15000元,B种防疫物资每箱12000元.若购买B种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:A、B两种防疫物资均需购买,并按整箱配送).23. 如图,在平面直角坐标系 中,反比例函数 的图像经过点 ,点B在y轴的负半轴上, 交x轴于点C,C为线段 的中点.
(1)、甲、乙两公司各有多少人?(2)、现甲、乙两公司共同使用这笔捐款购买A、B两种防疫物资,A种防疫物资每箱15000元,B种防疫物资每箱12000元.若购买B种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:A、B两种防疫物资均需购买,并按整箱配送).23. 如图,在平面直角坐标系 中,反比例函数 的图像经过点 ,点B在y轴的负半轴上, 交x轴于点C,C为线段 的中点.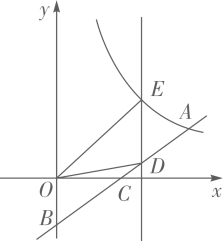 (1)、 , 点 的坐标为;(2)、若点D为线段 上的一个动点,过点D作 轴,交反比例函数图象于点E,求 面积的最大值.24. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
(1)、 , 点 的坐标为;(2)、若点D为线段 上的一个动点,过点D作 轴,交反比例函数图象于点E,求 面积的最大值.24. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
 (1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )25. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.
(1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )25. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.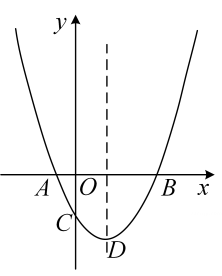
 (1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.26.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;
(1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.26.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;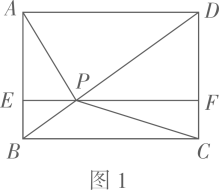 (2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
(2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);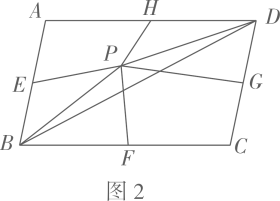 (3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
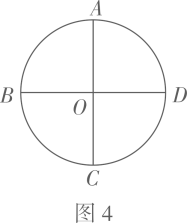
(3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);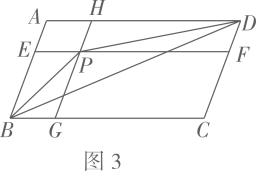 (4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).
(4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).