山东省枣庄市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 的绝对值是( )A、-2 B、 C、2 D、2. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
 A、10° B、15° C、18° D、30°3. 计算 的结果为( )A、 B、 C、 D、4. 实数a , b在数轴上对应点的位置如图所示,下列判断正确的是( )
A、10° B、15° C、18° D、30°3. 计算 的结果为( )A、 B、 C、 D、4. 实数a , b在数轴上对应点的位置如图所示,下列判断正确的是( )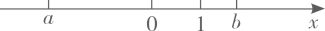 A、 B、 C、 D、5. 布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是( )A、 B、 C、 D、6. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
A、 B、 C、 D、5. 布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是( )A、 B、 C、 D、6. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )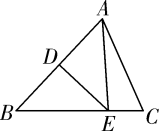 A、8 B、11 C、16 D、177. 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A、8 B、11 C、16 D、177. 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )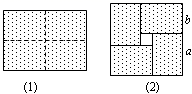 A、 B、 C、 D、8. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )
A、 B、 C、 D、8. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )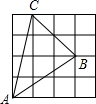 A、
A、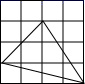 B、
B、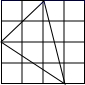 C、
C、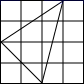 D、
D、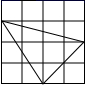 9. 对于实数 、 ,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: .则方程 的解是( )A、 B、 C、 D、10. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , ,将 绕点O逆时针旋转 ,点B的对应点B的坐标是( )
9. 对于实数 、 ,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: .则方程 的解是( )A、 B、 C、 D、10. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , ,将 绕点O逆时针旋转 ,点B的对应点B的坐标是( )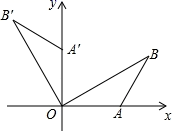 A、 B、 C、 D、11. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A、 B、 C、 D、11. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、512. 如图,已知抛物线 的对称轴为直线 .给出下列结论:
A、 B、6 C、4 D、512. 如图,已知抛物线 的对称轴为直线 .给出下列结论: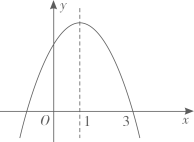
① ; ② ; ③ ; ④ .
其中,正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
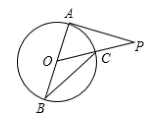
13. 若a+b=3,a2+b2=7,则ab= .14. 已知关于x的一元二次方程 有一个根为 ,则a的值为 .15. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 .
 16. 如图,人字梯AB,AC的长都为2米。当a=50°时,人字梯顶端高地面的高度AD是米(结果精确到0.1m。参考依据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
16. 如图,人字梯AB,AC的长都为2米。当a=50°时,人字梯顶端高地面的高度AD是米(结果精确到0.1m。参考依据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 17. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .
17. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .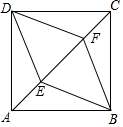 18. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
18. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
三、解答题
-
19. 解不等式组 ,并求它的所有整数解的和.20. 欧拉(Euler , 1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.(1)、观察下列多面体,并把下表补充完整:
名称
三棱锥
三棱柱
正方体
正八面体
图形
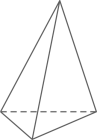
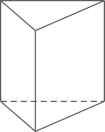
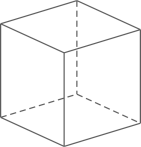

顶点数V
4
6
8
棱数E
6
12
面数F
4
5
8
(2)、分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式: .21. 2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.学生立定跳远测试成绩的频数分布表
分组
频数
a
12
b
10
学生立定跳远测试成绩的频数分布直方图

请根据图表中所提供的信息,完成下列问题:
(1)、表中 , ;(2)、样本成绩的中位数落在范围内;(3)、请把频数分布直方图补充完整;22. 如图,在平面直角坐标系 中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .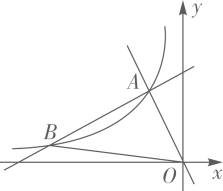 (1)、求反比例函数的表达式;(2)、设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.23. 如图,在 中, ,以AB为直径的 分别交AC、BC于点D、E , 点F在AC的延长线上,且 .
(1)、求反比例函数的表达式;(2)、设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.23. 如图,在 中, ,以AB为直径的 分别交AC、BC于点D、E , 点F在AC的延长线上,且 .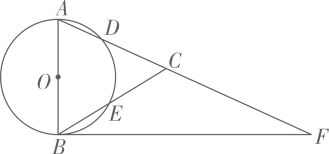 (1)、求证:BF是 的切线;(2)、若 的直径为4, ,求 .24. 在 中, ,CD是中线, ,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F , DF与AE交于点M , DE与BC交于点N .
(1)、求证:BF是 的切线;(2)、若 的直径为4, ,求 .24. 在 中, ,CD是中线, ,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F , DF与AE交于点M , DE与BC交于点N .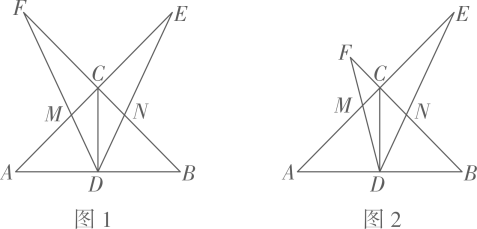 (1)、如图1,若 ,求证: ;(2)、如图2,在 绕点D旋转的过程中,试证明 恒成立;(3)、若 , ,求DN的长.25. 如图,抛物线 交x轴于 , 两点,与y轴交于点C , AC , BC . M为线段OB上的一个动点,过点M作 轴,交抛物线于点P , 交BC于点Q .
(1)、如图1,若 ,求证: ;(2)、如图2,在 绕点D旋转的过程中,试证明 恒成立;(3)、若 , ,求DN的长.25. 如图,抛物线 交x轴于 , 两点,与y轴交于点C , AC , BC . M为线段OB上的一个动点,过点M作 轴,交抛物线于点P , 交BC于点Q . (1)、求抛物线的表达式;(2)、过点P作 ,垂足为点N . 设M点的坐标为 ,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)、试探究点M在运动过程中,是否存在这样的点Q , 使得以A , C , Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、过点P作 ,垂足为点N . 设M点的坐标为 ,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)、试探究点M在运动过程中,是否存在这样的点Q , 使得以A , C , Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.