湖北省鄂州市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、选择题
-
1. -2020的相反数是( )A、2020 B、-2020 C、 D、-2. 下列运算正确的是( )A、 B、 C、 D、3. 如图是由5个小正方体组合成的几何体,则其俯视图为( )
 A、
A、 B、
B、 C、
C、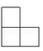 D、
D、 4. 面对2020年突如其来的新冠疫情,党和国家及时采取“严防严控”措施,并对新冠患者全部免费治疗.据统计共投入约21亿元资金.21亿用科学记数法可表示为( )A、 B、 C、 D、5. 如图, ,一块含 的直角三角板的一个顶点落在其中一条直线上,若 ,则 的度数为( )
4. 面对2020年突如其来的新冠疫情,党和国家及时采取“严防严控”措施,并对新冠患者全部免费治疗.据统计共投入约21亿元资金.21亿用科学记数法可表示为( )A、 B、 C、 D、5. 如图, ,一块含 的直角三角板的一个顶点落在其中一条直线上,若 ,则 的度数为( )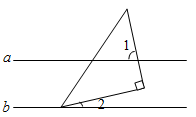 A、 B、 C、 D、6. 一组数据4,5,x,7,9的平均数为6,则这组数据的众数为( )A、4 B、5 C、7 D、97. 目前以 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 用户2万户,计划到2021年底全市 用户数累计达到8.72万户.设全市 用户数年平均增长率为 ,则 值为( )A、 B、 C、 D、8. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论:
A、 B、 C、 D、6. 一组数据4,5,x,7,9的平均数为6,则这组数据的众数为( )A、4 B、5 C、7 D、97. 目前以 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 用户2万户,计划到2021年底全市 用户数累计达到8.72万户.设全市 用户数年平均增长率为 ,则 值为( )A、 B、 C、 D、8. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论: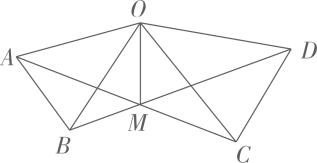
① ;② ;③ 平分 ;④ 平分
其中正确的结论个数有( )个.
A、4 B、3 C、2 D、19. 如图,抛物线 与 轴交于点 和B,与y轴交于点 .下列结论:① ;② ;③ ;④ ,其中正确的结论个数为( )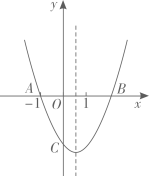 A、4 B、2个 C、3个 D、4个10. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 ,则 (n为正整数)的坐标是( )
A、4 B、2个 C、3个 D、4个10. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 ,则 (n为正整数)的坐标是( )
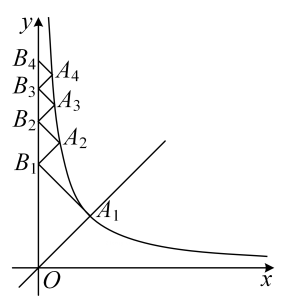 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: =.12. 关于x的不等式组 的解集是.13. 用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .14. 如图,点A是双曲线 上一动点,连接 ,作 ,且使 ,当点A在双曲线 上运动时,点B在双曲线 上移动,则k的值为.
 15. 如图,半径为 的 与边长为 的正方形 的边 相切于E,点F为正方形的中心,直线 过 点.当正方形 沿直线 以每秒 的速度向左运动秒时, 与正方形重叠部分的面积为 .
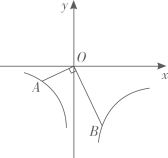
15. 如图,半径为 的 与边长为 的正方形 的边 相切于E,点F为正方形的中心,直线 过 点.当正方形 沿直线 以每秒 的速度向左运动秒时, 与正方形重叠部分的面积为 . 16. 如图,已知直线 与x、y轴交于A、B两点, 的半径为1,P为 上一动点, 切 于Q点.当线段 长取最小值时,直线 交y轴于M点,a为过点M的一条直线,则点P到直线a的距离的最大值为.
16. 如图,已知直线 与x、y轴交于A、B两点, 的半径为1,P为 上一动点, 切 于Q点.当线段 长取最小值时,直线 交y轴于M点,a为过点M的一条直线,则点P到直线a的距离的最大值为.
三、解答题
-
17. 先化简 ,再从 , ,0,1,2中选一个合适的数作为x的值代入求值.18. 如图,在平行四边形 中,对角线 与 交于点O,点M,N分别为 、 的中点,延长 至点E,使 ,连接 .
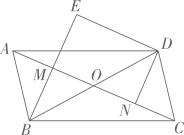 (1)、求证: ;(2)、若 ,且 , ,求四边形 的面积.19. 某校为了了解全校学生线上学习情况,随机选取该校部分学生,调查学生居家学习时每天学习时间(包括线上听课及完成作业时间).以下是根据调查结果绘制的统计图表.请你根据图表中的信息完成下列问题:
(1)、求证: ;(2)、若 ,且 , ,求四边形 的面积.19. 某校为了了解全校学生线上学习情况,随机选取该校部分学生,调查学生居家学习时每天学习时间(包括线上听课及完成作业时间).以下是根据调查结果绘制的统计图表.请你根据图表中的信息完成下列问题:频数分布表
学习时间分组
频数
频率
A组( )
9
m
B组( )
18
0.3
C组( )
18
0.3
D组( )
n
0.2
E组( )
3
0.05
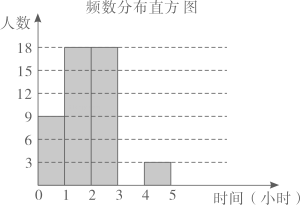 (1)、频数分布表中 , , 并将频数分布直方图补充完整;(2)、若该校有学生1000名,现要对每天学习时间低于2小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?(3)、已知调查的E组学生中有2名男生1名女生,老师随机从中选取2名学生进一步了解学生居家学习情况.请用树状图或列表求所选2名学生恰为一男生一女生的概率.20. 已知关于x的方程 有两实数根.(1)、求k的取值范围;(2)、设方程两实数根分别为 、 ,且 ,求实数k的值.21. 鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为 ,无人机沿水平线 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段 的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中 米.
(1)、频数分布表中 , , 并将频数分布直方图补充完整;(2)、若该校有学生1000名,现要对每天学习时间低于2小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?(3)、已知调查的E组学生中有2名男生1名女生,老师随机从中选取2名学生进一步了解学生居家学习情况.请用树状图或列表求所选2名学生恰为一男生一女生的概率.20. 已知关于x的方程 有两实数根.(1)、求k的取值范围;(2)、设方程两实数根分别为 、 ,且 ,求实数k的值.21. 鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为 ,无人机沿水平线 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段 的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中 米. (1)、求无人机的飞行高度 ;(结果保留根号)(2)、求河流的宽度 .(结果精确到1米,参考数据: )22. 如图所示: 与 的边 相切于点C,与 、 分别交于点D、E, . 是 的直径.连接 ,过C作 交 于G,连接 、 , 与 交于点F.
(1)、求无人机的飞行高度 ;(结果保留根号)(2)、求河流的宽度 .(结果精确到1米,参考数据: )22. 如图所示: 与 的边 相切于点C,与 、 分别交于点D、E, . 是 的直径.连接 ,过C作 交 于G,连接 、 , 与 交于点F.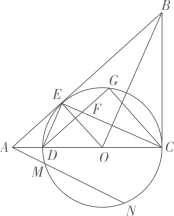 (1)、求证:直线 与 相切;(2)、求证: ;(3)、若 时,过A作 交 于M、N两点(M在线段 上),求 的长.23. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
(1)、求证:直线 与 相切;(2)、求证: ;(3)、若 时,过A作 交 于M、N两点(M在线段 上),求 的长.23. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x(元/件)
4
5
6
y(件)
10000
9500
9000
(1)、求y与x的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)、抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元( ),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.24. 如图,抛物线 与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线 经过B、C两点. (1)、求抛物线的解析式;(2)、点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线 及x轴分别交于点D、M. ,垂足为N.设 .
(1)、求抛物线的解析式;(2)、点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线 及x轴分别交于点D、M. ,垂足为N.设 .①点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m的值;
②当点P在直线 下方的抛物线上运动时,是否存在一点P,使 与 相似.若存在,求出点P的坐标;若不存在,请说明理由.