山东省潍坊市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 下列图形,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、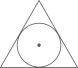 2. 下列运算正确的是( )A、 B、 C、 D、3. 今年的政府工作报告中指出:去年脱贫攻坚取得决定性成就,农村贫困人口减少1109万.数字1109万用科学记数法可表示为( )A、 B、 C、 D、4. 将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的左视图是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 今年的政府工作报告中指出:去年脱贫攻坚取得决定性成就,农村贫困人口减少1109万.数字1109万用科学记数法可表示为( )A、 B、 C、 D、4. 将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
5. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:一分钟跳绳个数(个)
141
144
145
146
学生人数(名)
5
2
1
2
则关于这组数据的结论正确的是( )
A、平均数是144 B、众数是141 C、中位数是144.5 D、方差是5.46. 若 ,则 的值是( )A、4 B、3 C、2 D、17. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )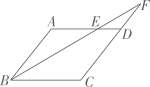 A、21 B、28 C、34 D、428. 关于x的一元二次方程 根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定9. 如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )
A、21 B、28 C、34 D、428. 关于x的一元二次方程 根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定9. 如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )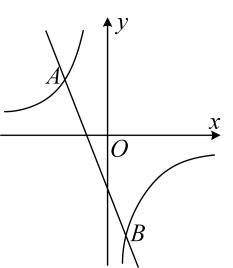 A、 B、 或 C、 D、 或10. 如图,在 中, ,以点O为圆心,2为半径的圆与 交于点C,过点C作 交 于点D,点P是边 上的动点.当 最小时, 的长为( )
A、 B、 或 C、 D、 或10. 如图,在 中, ,以点O为圆心,2为半径的圆与 交于点C,过点C作 交 于点D,点P是边 上的动点.当 最小时, 的长为( ) A、 B、 C、1 D、11. 若关于x的不等式组 有且只有3个整数解,则a的取值范围是( )A、 B、 C、 D、12. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、
A、 B、 C、1 D、11. 若关于x的不等式组 有且只有3个整数解,则a的取值范围是( )A、 B、 C、 D、12. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、 B、
B、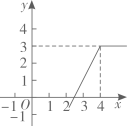 C、
C、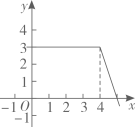 D、
D、
二、填空题
-
13. 因式分解:x2y﹣9y= .
14. 若 ,则 .15. 如图,在 中, , , 垂直平分 ,垂足为Q,交 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边 于点D,E;②分别以点D,E为圆心,以大于 的长为半径作弧,两弧相交于点F;⑤作射线 .若 与 的夹角为 ,则 °. 16. 若关于x的分式方程 有增根,则m= .17. 如图,矩形 中,点G,E分别在边 上,连接 ,将 和 分别沿 折叠,使点B,C恰好落在 上的同一点,记为点F.若 ,则 .
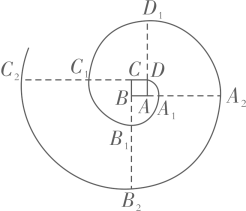
16. 若关于x的分式方程 有增根,则m= .17. 如图,矩形 中,点G,E分别在边 上,连接 ,将 和 分别沿 折叠,使点B,C恰好落在 上的同一点,记为点F.若 ,则 . 18. 如图,四边形 是正方形,曲线 是由一段段90度的弧组成的.其中: 的圆心为点A,半径为 ;
18. 如图,四边形 是正方形,曲线 是由一段段90度的弧组成的.其中: 的圆心为点A,半径为 ;的圆心为点B,半径为 ;
的圆心为点C,半径为 ;
的圆心为点D,半径为 ;…
的圆心依次按点A,B,C,D循环.若正方形 的边长为1,则 的长是 .
三、解答题
-
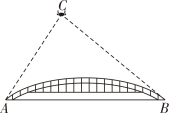
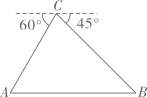
19. 先化简,再求值: ,其中x是16的算术平方根.20. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.
 21. 在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档: ;B档: ;C档: ;D档: .根据调查情况,给出了部分数据信息:
21. 在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档: ;B档: ;C档: ;D档: .根据调查情况,给出了部分数据信息:①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;
②图1和图2是两幅不完整的统计图.
根据以上信息解答问题:
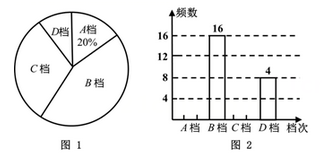 (1)、求本次调查的学生人数,并将图2补充完整;(2)、已知全校共1200名学生,请你估计全校B档的人数;(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.22. 如图, 为 的直径,射线 交 于点F,点C为劣弧 的中点,过点C作 ,垂足为E,连接 .
(1)、求本次调查的学生人数,并将图2补充完整;(2)、已知全校共1200名学生,请你估计全校B档的人数;(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.22. 如图, 为 的直径,射线 交 于点F,点C为劣弧 的中点,过点C作 ,垂足为E,连接 .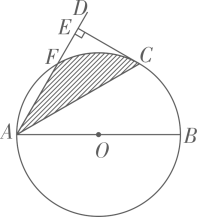 (1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.23. 因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量y(桶)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
(1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.23. 因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量y(桶)与销售单价x(元)之间满足一次函数关系,其图象如图所示. (1)、求y与x之间的函数表达式;(2)、每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利涧=销售价-进价)24. 如图1,在 中, ,点D,E分别在边 上,且 ,连接 .现将 绕点A顺时针方向旋转,旋转角为 ,如图2,连接 .
(1)、求y与x之间的函数表达式;(2)、每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利涧=销售价-进价)24. 如图1,在 中, ,点D,E分别在边 上,且 ,连接 .现将 绕点A顺时针方向旋转,旋转角为 ,如图2,连接 .
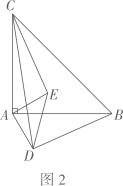
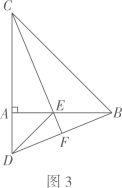 (1)、当 时,求证: ;(2)、如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;(3)、在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.25. 如图,抛物线 与x轴交于点 和点 ,与y轴交于点C,顶点为D,连接 与抛物线的对称轴l交于点E.
(1)、当 时,求证: ;(2)、如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;(3)、在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.25. 如图,抛物线 与x轴交于点 和点 ,与y轴交于点C,顶点为D,连接 与抛物线的对称轴l交于点E.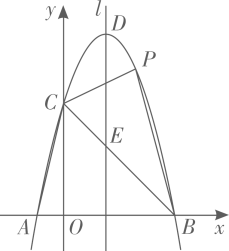 (1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接 ,当 时,求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线 上是否存在点M,使得以点M,N,E为顶点的三角形与 相似?若存在,求点M的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接 ,当 时,求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线 上是否存在点M,使得以点M,N,E为顶点的三角形与 相似?若存在,求点M的坐标;若不存在,请说明理由.