河南省2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、选择题
-
1. 2的相反数是( )A、 B、 C、2 D、-22. 如下摆放的几何体中,主视图与左视图有可能不同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 要调查下列问题,适合采用全面调查(普查)的是( )A、中央电视台《开学第--课》 的收视率 B、某城市居民6月份人均网上购物的次数 C、即将发射的气象卫星的零部件质量 D、某品牌新能源汽车的最大续航里程4. 如图, ,若 ,则 的度数为( )
3. 要调查下列问题,适合采用全面调查(普查)的是( )A、中央电视台《开学第--课》 的收视率 B、某城市居民6月份人均网上购物的次数 C、即将发射的气象卫星的零部件质量 D、某品牌新能源汽车的最大续航里程4. 如图, ,若 ,则 的度数为( ) A、 B、 C、 D、5. 电子文件的大小常用 等作为单位,其中 ,某视频文件的大小约为 等于( )A、 B、 C、 D、6. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、7. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根8. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( )
A、 B、 C、 D、5. 电子文件的大小常用 等作为单位,其中 ,某视频文件的大小约为 等于( )A、 B、 C、 D、6. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、7. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根8. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( )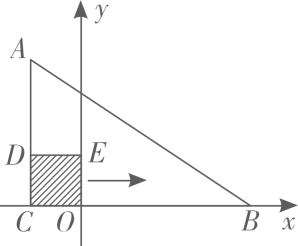 A、 B、 C、 D、10. 如图,在 中, ,分别以点 为圆心, 的长为半径作弧,两弧交于点D,连接 则四边形 的面积为( )
A、 B、 C、 D、10. 如图,在 中, ,分别以点 为圆心, 的长为半径作弧,两弧交于点D,连接 则四边形 的面积为( ) A、 B、9 C、6 D、
A、 B、9 C、6 D、二、填空题
-
11. 请写出一个大于1且小于2的无理数:.12. 已知关于 的不等式组 ,其中 在数轴上的对应点如图所示,则这个不等式组的解集为.
 13. 如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.
13. 如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是. 14. 如图,在边长为 的正方形 中,点 分别是边 的中点,连接 点 分别是 的中点,连接 ,则 的长度为.
14. 如图,在边长为 的正方形 中,点 分别是边 的中点,连接 点 分别是 的中点,连接 ,则 的长度为. 15. 如图,在扇形 中, 平分 交狐 于点D.点E为半径 上一动点若 ,则阴影部分周长的最小值为.
15. 如图,在扇形 中, 平分 交狐 于点D.点E为半径 上一动点若 ,则阴影部分周长的最小值为.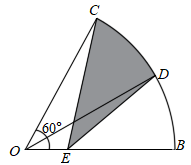
三、解答题
-
16. 先化简,再求值: ,其中17. 为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋 ,与之相差大于 为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:
[收集数据]从甲、乙两台机器分装的成品中各随机抽取 袋,测得实际质量(单位: )
如下:
甲:
乙:
[整理数据]整理以上数据,得到每袋质量 的频数分布表.
485≤x<490 490≤x<495 495≤x<500 500≤x<505 505≤x<510 510≤x<515 甲 2 2 4 7 4 1 乙 1 3 5 7 3 1 [分析数据]根据以上数据,得到以下统计量.

平均数 中位数 方差 不合格率 甲 499.7 501.5 42.01 b 乙 499.7 a 31.81 10% 根据以上信息,回答下列问题:
(1)、表格中的(2)、综合上表中的统计量,判断工厂应选购哪一台分装机,并说明理由.18. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水 平步道 上架设测角仪,先在点M处测得观星台最高点A的仰角为 ,然后沿 方向前进 到达点N处,测得点 的仰角为 .测角仪的高度为 ,
(1)、求观星台最高点A距离地面的高度(结果精确到 .参考数据: );(2)、“景点简介”显示,观星台的高度为 ,请计算本次测量结果的误差,并提出一条减小误差的合理化建议.19. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身x(次),按照方案一所需费用为 ,(元),且 ;按照方案二所需费用为 (元) ,且 其函数图象如图所示.
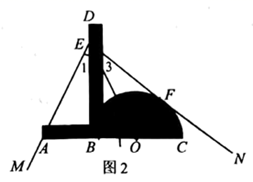
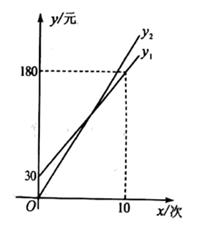 (1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.20. 我们学习过利用用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的人们根据实际需爱,发明了一种简易操作工具--------三分角器.图1是它的示意图,其中 与半圆O的直径 在同一直线 上,且 的长度与半圆的半径相等; 与 重直F点 足够长.
(1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.20. 我们学习过利用用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的人们根据实际需爱,发明了一种简易操作工具--------三分角器.图1是它的示意图,其中 与半圆O的直径 在同一直线 上,且 的长度与半圆的半径相等; 与 重直F点 足够长.使用方法如图2所示,若要把 三等分,只需适当放置三分角器,使 经过 的顶点 ,点 落在边 上,半圆O与另一边 恰好相切,切点为F,则 就把 三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.

已知:如图2,点在 同一直线上, 垂足为点B, ▲
求证: ▲
 21. 如图,抛物线 与x轴正半轴,y轴正半轴分别交于点 ,且 点G为抛物线的顶点.
21. 如图,抛物线 与x轴正半轴,y轴正半轴分别交于点 ,且 点G为抛物线的顶点. (1)、求抛物线的解析式及点G的坐标;(2)、点 为抛物线上两点(点M在点N的左侧) ,且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点 之间(含点 )的一个动点,求点Q的纵坐标 的取值范围.22. 小亮在学习中遇到这样一个问题:
(1)、求抛物线的解析式及点G的坐标;(2)、点 为抛物线上两点(点M在点N的左侧) ,且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点 之间(含点 )的一个动点,求点Q的纵坐标 的取值范围.22. 小亮在学习中遇到这样一个问题:如图,点D是弧 上一动点,线段 点A是线段 的中点,过点C作 ,交 的延长线于点F.当 为等腰三角形时,求线段 的长度.

小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:
(1)、根据点D在弧 上的不同位置,画出相应的图形,测量线段 的长度,得到下表的几组对应值.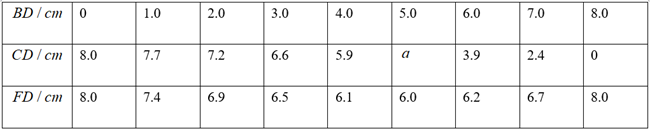
操作中发现:
①"当点D为弧 的中点时, ".则上中a的值是
②"线段 的长度无需测量即可得到".请简要说明理由;
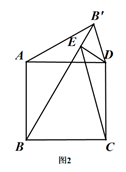
(2)、将线段 的长度作为自变量 和 的长度都是x的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;(3)、继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值.(结果保留一位小数).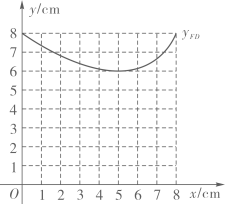 23. 将正方形 的边 绕点A逆时针旋转至 ,记旋转角为 .连接 ,过点D作 垂直于直线 ,垂足为点E,连接 ,(1)、如图1,当 时, 的形状为 ,连接 ,可求出 的值为;
23. 将正方形 的边 绕点A逆时针旋转至 ,记旋转角为 .连接 ,过点D作 垂直于直线 ,垂足为点E,连接 ,(1)、如图1,当 时, 的形状为 ,连接 ,可求出 的值为; (2)、当 且 时,
(2)、当 且 时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点 为顶点的四边形是平行四边形时,请直接写出 的值.