山东省临沂市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 下列温度比 低的是( )A、 B、 C、 D、2. 下列交通标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,数轴上点A对应的数是 ,将点A沿数轴向左移动2个单位至点B,则点B对应的数是( )
3. 如图,数轴上点A对应的数是 ,将点A沿数轴向左移动2个单位至点B,则点B对应的数是( )
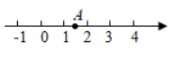 A、 B、-2 C、 D、4. 根据图中三视图可知该几何体是( )
A、 B、-2 C、 D、4. 根据图中三视图可知该几何体是( ) A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱5. 如图,在 中, , , ,则 ( )
A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱5. 如图,在 中, , , ,则 ( ) A、 B、 C、 D、6. 计算 的结果是( )A、 B、 C、 D、7. 设 ,则( )A、 B、 C、 D、8. 一元二次方程 的解是( )A、 , B、 , C、 , D、 ,9. 从马鸣、杨豪、陆畅,江宽四人中抽调两人参加“寸草心”志愿服务队,恰好抽到马鸣和杨豪的概率是( )A、 B、 C、 D、10. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、11. 下图是甲、乙两同学五次数学测试成绩的折线图,比较甲、乙的成绩,下列说法正确的是( )
A、 B、 C、 D、6. 计算 的结果是( )A、 B、 C、 D、7. 设 ,则( )A、 B、 C、 D、8. 一元二次方程 的解是( )A、 , B、 , C、 , D、 ,9. 从马鸣、杨豪、陆畅,江宽四人中抽调两人参加“寸草心”志愿服务队,恰好抽到马鸣和杨豪的概率是( )A、 B、 C、 D、10. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、11. 下图是甲、乙两同学五次数学测试成绩的折线图,比较甲、乙的成绩,下列说法正确的是( )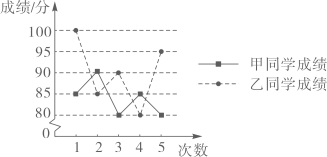 A、甲平均分高,成绩稳定 B、甲平均分高,成绩不稳定 C、乙平均分高,成绩稳定 D、乙平均分高,成绩不稳定12. 如图,P是面积为S的 内任意一点, 的面积为 , 的面积为 ,则( )
A、甲平均分高,成绩稳定 B、甲平均分高,成绩不稳定 C、乙平均分高,成绩稳定 D、乙平均分高,成绩不稳定12. 如图,P是面积为S的 内任意一点, 的面积为 , 的面积为 ,则( )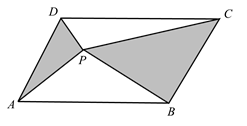 A、 B、 C、 D、 的大小与P点位置有关13. 计算 的结果为( )A、 B、 C、 D、14. 如图,在 中, 为直径, ,点D为弦 的中点,点E为 上任意一点,则 的大小可能是( )
A、 B、 C、 D、 的大小与P点位置有关13. 计算 的结果为( )A、 B、 C、 D、14. 如图,在 中, 为直径, ,点D为弦 的中点,点E为 上任意一点,则 的大小可能是( )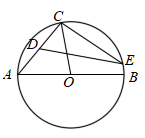 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
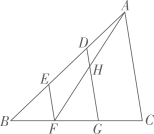
15. 不等式 的解集是 .16. 若 ,则 .17. 点 和点 在直线 上,则m与n的大小关系是 .18. 如图,在 中,D,E为边 的三等分点, ,H为 与 的交点.若 ,则 .
 19. 我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .
19. 我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .
三、解答题
-
20. 计算: .21. 2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:

质量
组中值
数量(只)
1.0
6
1.2
9
1.4
a
1.6
15
1.8
8
根据以上信息,解答下列问题:
(1)、表中 , 补全频数分布直方图;(2)、这批鸡中质量不小于 的大约有多少只?(3)、这些贫因户的总收入达到54000元,就能实现全员脱贫目标.按15元 的价格售出这批鸡后,该村贫困户能否脱贫?22. 如图.要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 一般要满足 ,现有一架长 的梯子.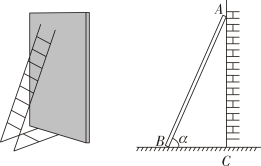 (1)、使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?(2)、当梯子底端距离墙面 时, 等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
(1)、使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?(2)、当梯子底端距离墙面 时, 等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?(参考数据: , , , , , )
23. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位: )是反比例函数关系.当 时, .(1)、写出I关于R的函数解析式;(2)、完成下表,并在给定的平面直角坐标系中画出这个函数的图象;…
…
…
…
 (3)、如果以此蓄电池为电源的用电器的限制电流不能超过 .那么用电器可变电阻应控制在什么范围内?24. 已知 的半径为 , 的半径为 ,以 为圆心,以 的长为半径画弧,再以线段 的中点P为圆心,以 的长为半径画弧,两弧交于点A,连接 , , 交 于点B,过点B作 的平行线 交 于点C.
(3)、如果以此蓄电池为电源的用电器的限制电流不能超过 .那么用电器可变电阻应控制在什么范围内?24. 已知 的半径为 , 的半径为 ,以 为圆心,以 的长为半径画弧,再以线段 的中点P为圆心,以 的长为半径画弧,两弧交于点A,连接 , , 交 于点B,过点B作 的平行线 交 于点C.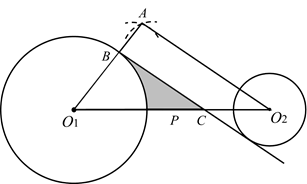 (1)、求证: 是 的切线;(2)、若 , , ,求阴影部分的面积.
(1)、求证: 是 的切线;(2)、若 , , ,求阴影部分的面积.
