山东省聊城2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 在实数-1, ,0, 中,最小的实数是( ).A、-1 B、 C、0 D、2. 如图所示的几何体的俯视图是( )
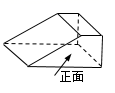 A、
A、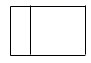 B、
B、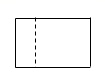 C、
C、 D、
D、 3. 如图,在 ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
3. 如图,在 ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )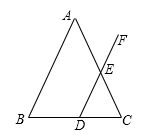 A、120° B、130° C、145° D、150°4. 下列计算正确的是( ).A、 B、 C、 D、5. 为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是( )
A、120° B、130° C、145° D、150°4. 下列计算正确的是( ).A、 B、 C、 D、5. 为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是( )成绩/分
84
88
92
96
100
人数/人
2
4
9
10
5
A、92分,96分 B、94分,96分 C、96分,96分 D、96分,100分6. 计算 的结果正确的是( ).A、1 B、 C、5 D、97. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ). A、 B、 C、 D、8. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、9. 如图, 是 的直径,弦 ,垂足为点M.连接 , .如果 , ,那么图中阴影部分的面积是( ).
A、 B、 C、 D、8. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、9. 如图, 是 的直径,弦 ,垂足为点M.连接 , .如果 , ,那么图中阴影部分的面积是( ).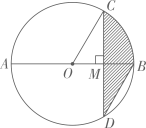 A、π B、2π C、3π D、4π10. 如图,有一块半径为1m,圆心角为 的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为( ).
A、π B、2π C、3π D、4π10. 如图,有一块半径为1m,圆心角为 的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为( ). A、 B、 C、 D、11. 人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成,如图中的每一个小正方形表示一块地砖.如果按图①②③…的次序铺设地砖,把第n个图形用图
A、 B、 C、 D、11. 人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成,如图中的每一个小正方形表示一块地砖.如果按图①②③…的次序铺设地砖,把第n个图形用图 表示,那么图㊿中的白色小正方形地砖的块数是( ).
表示,那么图㊿中的白色小正方形地砖的块数是( ).


 …A、150 B、200 C、355 D、50512. 如图,在 中, , ,将 绕点 旋转得到 ,使点 的对应点 落在 上,在 上取点 ,使 ,那么点 到 的距离等于( ).
…A、150 B、200 C、355 D、50512. 如图,在 中, , ,将 绕点 旋转得到 ,使点 的对应点 落在 上,在 上取点 ,使 ,那么点 到 的距离等于( ).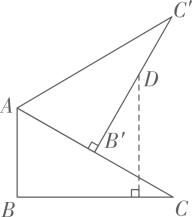 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
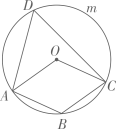
13. 因式分解: .14. 如图,在 中,四边形 为菱形,点 在 上,则 的度数是 .
 15. 某校开展读书日活动,小亮和小莹分别从校图书馆的“科技”、“文学”、“艺术”三类书籍中随机地抽取一本,抽到同一类书籍的概率是 .16. 如图,在直角坐标系中,点 , 是第一象限角平分线上的两点,点C的纵坐标为1,且 ,在 轴上取一点D,连接 , , , ,使得四边形 的周长最小,这个最小周长的值为 .
15. 某校开展读书日活动,小亮和小莹分别从校图书馆的“科技”、“文学”、“艺术”三类书籍中随机地抽取一本,抽到同一类书籍的概率是 .16. 如图,在直角坐标系中,点 , 是第一象限角平分线上的两点,点C的纵坐标为1,且 ,在 轴上取一点D,连接 , , , ,使得四边形 的周长最小,这个最小周长的值为 .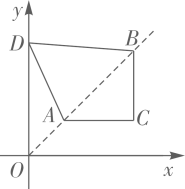
三、解答题
-
17. 计算: .18. 解不等式组 ,并写出它的所有整数解.19. 为了提高学生的综合素养,某校开设了五门手工活动课.按照类别分为:A“剪纸”、B“沙画”、C“葫芦雕刻”、D“泥塑”、E“插花”.为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如下两幅不完整的统计图.
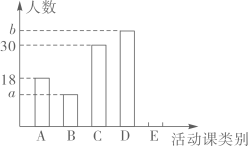
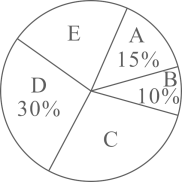
根据以上信息,回答下列问题:
(1)、本次调查的样本容量为;统计图中的 , ;(2)、通过计算补全条形统计图;(3)、该校共有2500名学生,请你估计全校喜爱“葫芦雕刻”的学生人数.20. 今年植树节期间,某景观园林公司购进一批成捆的A,B两种树苗,每捆 种树苗比每捆B种树苗多10棵,每捆A种树苗和每捆B种树苗的价格分别是630元和600元,而每棵A种树苗和每棵B种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.(1)、求这一批树苗平均每棵的价格是多少元?(2)、如果购进的这批树苗共5500棵,A种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进A种树苗和B种树苗各多少棵?并求出最低费用.21. 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F , 且AF=AD , 连接BF , 求证:四边形ABFC是矩形. 22. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
22. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)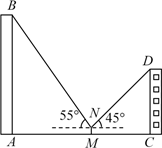 23. 如图,已知反比例函数 的图象与直线 相交于点 , .
23. 如图,已知反比例函数 的图象与直线 相交于点 , . (1)、求出直线 的表达式;(2)、在x轴上有一点 使得 的面积为18,求出点P的坐标.24. 如图,在 ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)、求出直线 的表达式;(2)、在x轴上有一点 使得 的面积为18,求出点P的坐标.24. 如图,在 ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.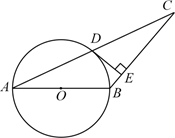 (1)、试证明DE是⊙O的切线;(2)、若⊙O的半径为5,AC=6 ,求此时DE的长.25. 如图,二次函数y=ax2+bx+4的图象与x轴交于点A(-1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)、试证明DE是⊙O的切线;(2)、若⊙O的半径为5,AC=6 ,求此时DE的长.25. 如图,二次函数y=ax2+bx+4的图象与x轴交于点A(-1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点. (1)、求出二次函数y=ax2+bx+4和BC所在直线的表达式;(2)、在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;(3)、连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与 DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
(1)、求出二次函数y=ax2+bx+4和BC所在直线的表达式;(2)、在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;(3)、连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与 DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.