山东省德州市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 的结果是( )A、 B、2020 C、 D、-20202. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图1是用5个相同的正方体搭成的立体图形,若由图1变化至图2,则三视图中没有发生变化的是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图1是用5个相同的正方体搭成的立体图形,若由图1变化至图2,则三视图中没有发生变化的是( )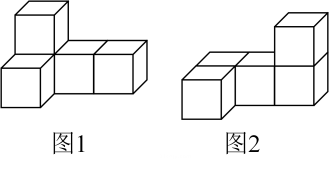 A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图5. 为提升学生的自理和自立能力,李老师调查了全班学生在一周内的做饭次数情况,调查结果如下表:
A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图5. 为提升学生的自理和自立能力,李老师调查了全班学生在一周内的做饭次数情况,调查结果如下表:一周做饭次数
4
5
6
7
8
人数
7
6
12
10
5
那么一周内该班学生的平均做饭次数为( )
A、4 B、5 C、6 D、76. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为( )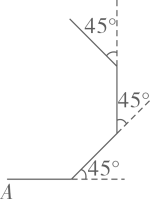 A、80米 B、96米 C、64米 D、48米7. 函数 和 在同一平面直角坐标系中的大致图象可能是( )A、
A、80米 B、96米 C、64米 D、48米7. 函数 和 在同一平面直角坐标系中的大致图象可能是( )A、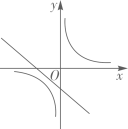 B、
B、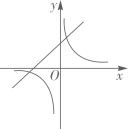 C、
C、 D、
D、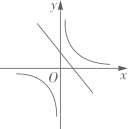 8. 下列命题:
8. 下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相垂直且平分的四边形是菱形;③一个角为90°且一组邻边相等的四边形是正方形;④对角线相等的平行四边形是矩形.其中真命题的个数是( )
A、1 B、2 C、3 D、49. 若关于x的不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、10. 如图,圆内接正六边形的边长为4,以其各边为直径作半圆,则图中阴影部分的面积为( ) A、 B、 C、 D、11. 二次函数 的部分图象如图所示,则下列选项错误的是( )
A、 B、 C、 D、11. 二次函数 的部分图象如图所示,则下列选项错误的是( )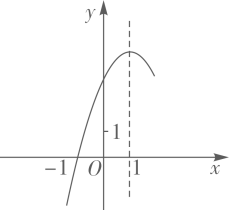 A、若 , 是图象上的两点,则 B、 C、方程 有两个不相等的实数根 D、当 时,y随x的增大而减小12. 下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )
A、若 , 是图象上的两点,则 B、 C、方程 有两个不相等的实数根 D、当 时,y随x的增大而减小12. 下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )


 A、148 B、152 C、174 D、202
A、148 B、152 C、174 D、202二、填空题
-
13. 计算: =.14. 若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是°.15. 在平面直角坐标系中,点A的坐标是 ,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数的解析式为 .16. 菱形的一条对角线长为8,其边长是方程 的一个根,则该菱形的周长为 .17. 如图,在 的正方形网格中,有4个小正方形已经涂黑,若再涂黑任意1个白色的小正方形(每个白色小正方形被涂黑的可能性相同),使新构成的黑色部分图形是轴对称图形的概率是 .
 18. 如图,在矩形ABCD中, , ,把AD沿AE折叠,使点D恰好落在AB边上的 处,再将 绕点E顺时针旋转 ,得到 ,使得 恰好经过 的中点F . 交AB于点G , 连接 有如下结论:① 的长度是 ;②弧 的长度是 ;③ ;④ .上述结论中,所有正确的序号是 .
18. 如图,在矩形ABCD中, , ,把AD沿AE折叠,使点D恰好落在AB边上的 处,再将 绕点E顺时针旋转 ,得到 ,使得 恰好经过 的中点F . 交AB于点G , 连接 有如下结论:① 的长度是 ;②弧 的长度是 ;③ ;④ .上述结论中,所有正确的序号是 .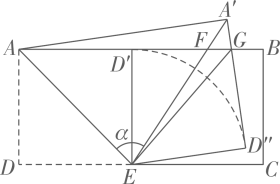
三、解答题
-
19. 先化简: ,然后选择一个合适的x值代入求值.20. 某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
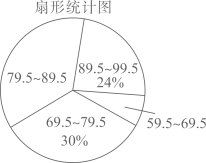
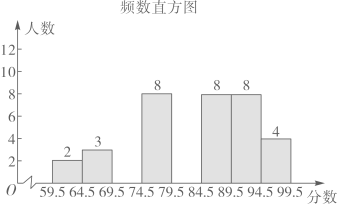 (1)、本次比赛参赛选手共有人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为;(2)、补全图2频数直方图;(3)、赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;(4)、成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.21. 如图,无人机在离地面60米的C处,观测楼房顶部B的俯角为30°,观测楼房底部A的俯角为60°,求楼房的高度.
(1)、本次比赛参赛选手共有人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为;(2)、补全图2频数直方图;(3)、赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;(4)、成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.21. 如图,无人机在离地面60米的C处,观测楼房顶部B的俯角为30°,观测楼房底部A的俯角为60°,求楼房的高度.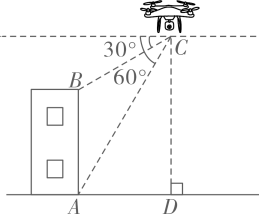 22. 如图,点C在以AB为直径的 上,点D是半圆AB的中点,连接AC , BC , AD , BD , 过点D作 交CB的延长线于点H .
22. 如图,点C在以AB为直径的 上,点D是半圆AB的中点,连接AC , BC , AD , BD , 过点D作 交CB的延长线于点H .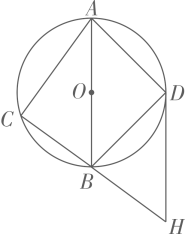 (1)、求证:直线DH是 的切线;(2)、若 , ,求AD , BH的长.23. 小刚去超市购买画笔,第一次花60元买了若干支A型画笔,第二次超市推荐了B型画笔,但B型画笔比A型画笔的单价贵2元,他又花100元买了相同支数的B型画笔.(1)、超市B型画笔单价多少元?(2)、小刚使用两种画笔后,决定以后使用B型画笔,但感觉其价格稍贵,和超市沟通后,超市给出以下优惠方案:一次购买不超过20支,则每支B型画笔打九折;若一次购买超过20支,则前20支打九折,超过的部分打八折.设小刚购买的B型画笔x支,购买费用为y元,请写出y关于x的函数关系式.(3)、在(2)的优惠方案下,若小刚计划用270元购买B型画笔,则能购买多少支B型画笔?24. 问题探究:
(1)、求证:直线DH是 的切线;(2)、若 , ,求AD , BH的长.23. 小刚去超市购买画笔,第一次花60元买了若干支A型画笔,第二次超市推荐了B型画笔,但B型画笔比A型画笔的单价贵2元,他又花100元买了相同支数的B型画笔.(1)、超市B型画笔单价多少元?(2)、小刚使用两种画笔后,决定以后使用B型画笔,但感觉其价格稍贵,和超市沟通后,超市给出以下优惠方案:一次购买不超过20支,则每支B型画笔打九折;若一次购买超过20支,则前20支打九折,超过的部分打八折.设小刚购买的B型画笔x支,购买费用为y元,请写出y关于x的函数关系式.(3)、在(2)的优惠方案下,若小刚计划用270元购买B型画笔,则能购买多少支B型画笔?24. 问题探究:小红遇到这样一个问题:如图1, 中, , ,AD是中线,求AD的取值范围.她的做法是:延长AD到E , 使 ,连接BE , 证明 ,经过推理和计算使问题得到解决.

请回答:
(1)、小红证明 的判定定理是:;(2)、AD的取值范围是;(3)、方法运用:如图2,AD是 的中线,在AD上取一点F , 连结BF并延长交AC于点E , 使 ,求证: .
(4)、如图3,在矩形ABCD中, ,在BD上取一点F , 以BF为斜边作 ,且 ,点G是DF的中点,连接EG , CG , 求证: .25. 如图1,在平面直角坐标系中,点A的坐标是 ,在x轴上任取一点M . 连接AM , 分别以点A和点M为圆心,大于 的长为半径作弧,两弧相交于G , H两点,作直线GH , 过点M作x轴的垂线l交直线GH于点P . 根据以上操作,完成下列问题.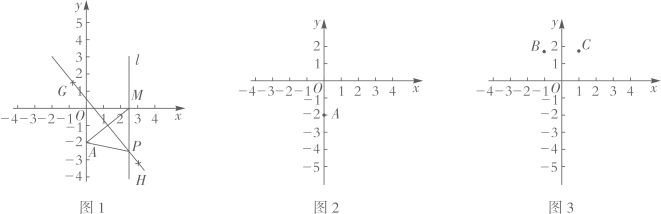
探究:
(1)、线段PA与PM的数量关系为 , 其理由为: .(2)、在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:M的坐标
…
…
P的坐标
…
…
(3)、请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L , 猜想曲线L的形状是 .(4)、验证:设点P的坐标是 ,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
(5)、应用:如图3,点 , ,点D为曲线L上任意一点,且 ,求点D的纵坐标 的取值范围.