2020年暑期衔接训练青岛版数学八年级下册：第19讲 一次函数的应用
试卷更新日期：2020-07-28 类型：复习试卷
一、单选题
-
1. 向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是 （ ）A、
B、
C、
D、
2. 某工厂加工一批零件，为了提高工人工作积极性，工厂规定每名工人每天薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的（ ）
A、a=20 B、b=4 C、若工人甲一天获得薪金180元，则他共生产45件． D、人乙一天生产40（件），则他获得薪金140元3. 某商店有一款畅销服装原价为40元，该商店规定：若顾客购买服装数量在20件以内，则按原价进行销售：若顾客购买服装数量超过20件，超过的部分每件可以享受指定的折扣，现八 班同学为参加学校秋季运动会，准备统一向该商店购买该款服装，所需费用 元 与购买数量 件 之间的函数关系如图所示，那么购买数量超过20件的部分每件享受到的折扣是
A、9折 B、8折 C、 折 D、7折4. 甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象的一部分如图所示．下列结论正确的个数是（ ）
（1）t＝5时，s＝150；（2）t＝35时，s＝450；（3）甲的速度是30米/分；（4）t＝12.5时，s＝0．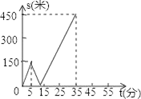
A、1个 B、2个 C、3个 D、4个5. 甲、乙两车沿同一平直公路由A地匀速行驶（中途不停留）前往终点B地，甲、乙两车的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示，小红通过图象得出以下4个信息：①甲车速度为60千米/小时；②A、B两地相距240千米；③乙车行驶2小时追上甲车；④乙车由A地到B地共用3小时．上述信息正确的有（ ）个．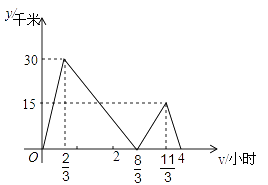
A、1 B、2 C、3 D、46. 甲、乙两车同时分别从 A，B 两处出发，沿直线 AB 作匀速运动，同时到达C 处，B 在 AC 上，甲的速度是乙的速度的1.5 倍，设 t(分)后甲、 乙两遥控车与 B 处的距离分别为 d1 ， d2 ， 且 d1 ， d2 与出发时间 t 的函数关系如图，那么在两车相遇前，两车与 B 点的距离相等时，t 的值为（ ）
A、0.4 B、0.5 C、0.6 D、17.如图，点A的坐标为（﹣2，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为（ ）
A、（ ， -） B、（- ， -） C、（0，0） D、（﹣1，﹣1）8. 如图是本地区一种产品30天的销售图像，图1是产品销售量y(件)与时间t(天)的函数关系，图2是一件产品的销售利润z(元)与时间t(天)的函数关系，已知日销售利润=日销售量×每件产品的销售利润，下列结论不正确的是（ ）。
A、第24天的销售量为200件 B、第10天销售一件产品的利润是15元 C、第12天与第30天这两天的日销售利润相等 D、第30天的日销售利润是750元9. 甲、乙两车从A地出发，沿同一路线驶向B地．甲车先出发匀速驶向B地，40min后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时．由于满载货物，为了行驶安全，速度减少了50km/h，结果与甲车同时到达B地．甲乙两车距A地的路程y（km）与乙车行驶时间x（h）之间的函数图象如图所示，则下列说法中正确的有（ ）① ；②甲的速度是60km/h；③乙出发80min追上甲；④乙刚到达货站时，甲距B地180km．
A、4个 B、3个 C、2个 D、1个10. 6月份以来，猪肉价格一路上涨．为平抑猪肉价格，某省积极组织货源，计划由A、B、C三市分别组织10辆、10辆和8辆运输车向D、E两市运送猪肉，现决定派往D、E两地的运输车分别是18辆、10辆，已知一辆运输车从A市到D、E两市的运费分别是200元和800元，从B市到D、E两市的运费分别是300元和700元，从C市到D、E两市的运费分别是400元和500元．若设从A、B两市都派x辆车到D市，则当这28辆运输车全部派出时，总运费W（元）的最小值和最大值分别是（ ）A、8000，13200 B、9000，10000 C、10000，13200 D、13200，1540011. 已知A、B两地相距630千米，在A、B之间有汽车站C站，如图1所示．客车由A地驶向C站、货车由B地驶向A地，两车同时出发，匀速行驶，货车的速度是客车速度的 ．图2是客、货车离C站的路程y1、y2（千米）与行驶时间x（小时）之间的函数关系图象．则下列说法不正确的是（ ）
A、货车行驶2小时到达C站 B、货车行驶完全程用时14小时 C、图2中的点E的坐标是（7，180） D、客车的速度是60千米∕时12. “龟兔首次赛跑”之后，输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事（ 表示乌龟从起点出发所行的时间， 表示乌龟所行的路程， 表示兔子所行的路程.下列说法中：①“龟兔再次赛跑”的路程为1000米；②兔子和乌龟同时从起点出发；③乌龟在途中休息了10分钟；④兔子在途中750米处上了乌龟.正确的有（ ）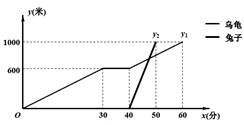
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 某商店卖水果，数量x(千克)与售价y(元)之间的关系如下表，(y是x的次函数)：
x/千克
0.5
1
1.5
2
…
y/元
1.6+0.1
3.2+0.1
4.8+0.1
6.4+0.1
当x=7千克时，售价y=元。
14. 某地出租车行驶里程 （ ）与所需费用 （元）的关系如图.若某乘客一次乘坐出租车里程12 ，则该乘客需支付车费元.
15. AB两地相距20km，甲从A地出发向B地前进，乙从B地出发向A地前进，两人沿同一直线同时出发，甲先以8km/h的速度前进1小时，然后减慢速度继续匀速前进，甲乙两人离A地的距离S（km）与时间t（h）的关系如图所示，则甲出发小时后与乙相遇．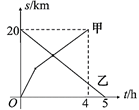
16. 如图，一次函数 y = kx + b 的图象与 x 轴的交点坐标为(2，0)，则下列说法：① y 随 x 的增大而增大；② b>0；③关于 x 的方程 kx+b=0的解为x=2；④不等式kx+b>0的解集是 x>2.其中说法正确有（把你认为说法正确序号都填上）.
17. 甲、乙两名大学生去距学校36千米的某乡镇进行社会调查．他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回．乙取相机后（在学校取相机所用时间忽略不计），骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为t（分钟）．y甲、y乙与x之间的函数图象如图所示，则乙返回到学校时，甲与学校相距千米．
18. 如图，在平面直角坐标系中，一次函数y=x+3 的图象与x轴交于点A，与y轴交于点B，点P在线段AB上，PC⊥x轴于点C，则△PCO周长的最小值为。
19. 如图所示的图像反映的过程是：甲乙两人同时从 地出发，以各自的速度匀速向 地行驶，甲先到 地停留半小时后，按原路以另一速度匀速返回，直至与乙相遇.乙的速度为 ， 表示甲乙两人相距的距离， 表示乙行驶的时间.现有以下 个结论：① 、 两地相距 ；②点 的坐标为 ；③甲去时的速度为 ；④甲返回的速度是 .以上 个结论中正确的是.
20. “双11”当天，重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件，该公司共有甲、乙、丙三种车型，其中甲型车数量占公司车辆总数的 ，乙型车辆是丙型车数量的2倍，上午安排甲车数量的 ，乙车数量的 ，丙车数量的 进行运输，且上午甲、乙、丙三种车型每辆载货量分别为15吨，10吨，20吨，则上午刚好运完当天全部快件重量的 ；下午安排剩下的所有车辆运输完当天剩下的所有快件，且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨，12吨，16吨，下午乙型车实际载货量为下午甲型车每辆实际载货量的 .已知同种货车每辆的实际载货量相等，甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨，90元/吨，60元/吨.则下午运输时，一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.三、计算题
-
21. 一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示.
(1)、求y关于x的函数关系式；(2)、已知当油箱中的剩余油量为8升时，该汽车会开始提示加油.在此次行驶过程中，行驶了450千米时，司机发现离前方最近的加油站有75千米的路程.在开往该加油站的途中，当汽车开始提示加油时，离加油站的路程是多少千米？四、解答题
-
22. 为倡导绿色出行，某共享单车近期登陆徐州，根据连续骑行时长分段计费：骑行时长在2h以内（含2h）的部分，每0.5h计费1元（不足0.5h按0.5h计算）； 骑行时长超出2h的部分，每小时计费4元（不足1h按1h计算）．
根据此收费标准，解决下列问题：
(1)、连续骑行5h，应付费多少元？(2)、若连续骑行xh（x＞2且x为整数） 需付费y元，则y与x的函数表达式为；(3)、若某人连续骑行后付费24元，求其连续骑行时长的范围．五、综合题
-
23. 快车和慢车分别从甲、乙两地同时出发，匀速相向而行，快车到达乙地后，慢车继续前行，设出发 小时后，两车相距 千米，图中折线表示从两车出发至慢车到达甲地的过程中 与 之间的函数关系式，根据图中信息，解答下列问题.
(1)、甲、乙两地相距千米，快车从甲地到乙地所用的时间是小时；(2)、求线段 的函数解析式（写出自变量取值范围），并说明点 的实际意义.(3)、求快车和慢车的速度.24. 某蛋糕店为了吸引顾客，在A、B两种蛋糕中，轮流降低其中一种蛋糕价格，这样形成两种盈利模式，模式一：A种蛋糕利润每盒8元，B种蛋糕利润每盒15元；模式二：A种蛋糕利润每盒14元，B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒，且都能售完，设每天销售A种蛋糕x盒(1)、设按模式一销售A、B两种蛋糕所获利润为y1元，按模式二销售A、B两种蛋糕所获利润为y2元，分别求出y1、y2关于x的函数解析式；(2)、在同一个坐标系内分别画出(1)题中的两个函数的图象；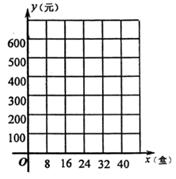
(3)、若y始终表示y1、y2中较大的值，请问y是否为x的函数，并说说你的理由，并直接写出y的最小值．25.在平面直角坐标系中，一次函数的图象与坐标轴围成的三角形，叫做此一次函数的坐标三角形．例如，图中的一次函数的图象与x，y轴分别交于点A，B，则△OAB为此函数的坐标三角形．
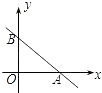(1)、求函数y= x+3的坐标三角形的三条边长；(2)、若函数y= x+b（b为常数）的坐标三角形周长为16，求此三角形面积．26. “节能环保，低碳生活”是我们倡导的一种生活方式．某家电商场计划用12万元购进节能型电视机、洗衣机和空调共40台．三种家电的进价及售价如表所示：种类
进价（元/台）
售价（元/台）
电视机
5000
5480
洗衣机
2000
2280
空 调
2500
2800
(1)、在不超出现有资金的前提下，若购进电视机的数量和洗衣机的数量相同，空调的数量不超过电视机的数量的三倍．请问商场有哪几种进货方案？
(2)、在“2016年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动．在（1）的条件下，若三种电器在活动期间全部售出，商家预计最多送出消费券多少张？
27. 某服装店的一次性购进甲、乙两种童衣共100件进行销售，其中甲种童衣的进价为80元/件，售价为120元/件；乙种童衣的进价为100元/件，售价为150元/件。设购进甲种童衣的数量为 （件），销售完这批童衣的总利润为 （元）。(1)、请求出 与 之间的函数关系式（不用写出 的取值范围）；(2)、如果购进的甲种童衣的件数不少于乙种童衣件数的3倍，求购进甲种童衣多少件式，这批童衣销售完利润最多？最多可以获利多少元？28. 某商店销售A型和B型两种型号的电脑，销售一台A型电脑可获利120元，销售一台B型电脑可获利140元．该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的3倍．设购进A型电脑x台，这100台电脑的销售总利润为y元．(1)、求y与x的关系式；(2)、该商店购进A型、B型电脑各多少台，才能使销售利润最大？(3)、若限定商店最多购进A型电脑60台，则这100台电脑的销售总利润能否为13600元？若能，请求出此时该商店购进A型电脑的台数；若不能，请求出这100台电脑销售总利润的范围．
-
-