湖南省岳阳市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. -2020的相反数是( )A、2020 B、-2020 C、 D、-2. 2019年以来,我国扶贫攻坚取得关键进展,农村贫困人口减少11090000人,数据11090000用科学记数法表示为( )A、 B、 C、 D、3. 如图,由4个相同正方体组成的几何体,它的左视图是( )
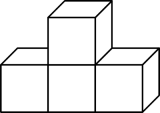 A、
A、 B、
B、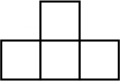 C、
C、 D、
D、 4. 下列运算结果正确的是( )A、 B、 C、 D、5. 如图, , , ,则 的度数是( )
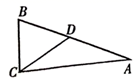
4. 下列运算结果正确的是( )A、 B、 C、 D、5. 如图, , , ,则 的度数是( )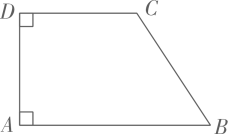 A、 B、 C、 D、6. 今年端午小长假复课第一天,学校根据疫情防控要求,对所有进入校园的师生进行体温检测,其中7名学生的体温(单位: )如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数和中位数分别是( )A、36.3,36.5 B、36.5,36.5 C、36.5,36.3 D、36.3,36.77. 下列命题是真命题的是( )A、一个角的补角一定大于这个角 B、平行于同一条直线的两条直线平行 C、等边三角形是中心对称图形 D、旋转改变图形的形状和大小8. 对于一个函数,自变量x取c时,函数值 等于0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 ,关于x的方程 有两个不相等的非零实数根 ,则下列关系式一定正确的是( )A、 B、 C、 D、
A、 B、 C、 D、6. 今年端午小长假复课第一天,学校根据疫情防控要求,对所有进入校园的师生进行体温检测,其中7名学生的体温(单位: )如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数和中位数分别是( )A、36.3,36.5 B、36.5,36.5 C、36.5,36.3 D、36.3,36.77. 下列命题是真命题的是( )A、一个角的补角一定大于这个角 B、平行于同一条直线的两条直线平行 C、等边三角形是中心对称图形 D、旋转改变图形的形状和大小8. 对于一个函数,自变量x取c时,函数值 等于0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 ,关于x的方程 有两个不相等的非零实数根 ,则下列关系式一定正确的是( )A、 B、 C、 D、二、填空题
-
9. 因式分解: .10. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .11. 不等式组 的解集是 .12. 如图:在 中,CD是斜边AB上的中线,若 ,则 .
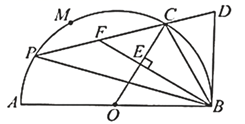
 13. 在 , ,1,2,3五个数中随机选取一个数作为二次函数 中a的值,则该二次函数图象开口向上的概率是 .14. 已知 ,则代数式 的值为 .15. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为 .16. 如图, 为半⊙O的直径,M,C是半圆上的三等分点, , 与半⊙O相切于点B,点 为 上一动点(不与点A,M重合),直线 交 于点D, 于点E,延长 交 于点F,则下列结论正确的是 . (写出所有正确结论的序号)
13. 在 , ,1,2,3五个数中随机选取一个数作为二次函数 中a的值,则该二次函数图象开口向上的概率是 .14. 已知 ,则代数式 的值为 .15. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为 .16. 如图, 为半⊙O的直径,M,C是半圆上的三等分点, , 与半⊙O相切于点B,点 为 上一动点(不与点A,M重合),直线 交 于点D, 于点E,延长 交 于点F,则下列结论正确的是 . (写出所有正确结论的序号)① ;② 的长为 ;③ ;④ ;⑤ 为定值.
三、解答题
-
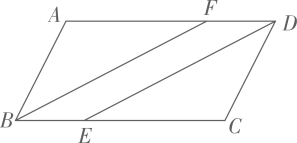
17. 计算:18. 如图,点E,F在 的边 , 上, , ,连接 , .求证:四边形 是平行四边形.
 19. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.
19. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.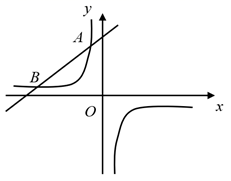 (1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.20. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图:
(1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.20. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图: (1)、本次随机调查的学生人数为人;(2)、补全条形统计图;(3)、若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;(4)、七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.21. 为做好复工复产,某工厂用A、B两种型号机器人搬运原料,已知A型机器人比B型机器人每小时多搬运 ,且A型机器人搬运 所用时间与B型机器人搬运 所用时间相等,求这两种机器人每小时分别搬运多少原料.
(1)、本次随机调查的学生人数为人;(2)、补全条形统计图;(3)、若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;(4)、七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.21. 为做好复工复产,某工厂用A、B两种型号机器人搬运原料,已知A型机器人比B型机器人每小时多搬运 ,且A型机器人搬运 所用时间与B型机器人搬运 所用时间相等,求这两种机器人每小时分别搬运多少原料. 22. 共抓长江大保护,建设水墨丹青新岳阳,推进市中心城区污水系统综合治理项目,需要从如图A,B两地向 地新建 , 两条笔直的污水收集管道,现测得C地在A地北偏东 方向上,在B地北偏西 方向上, 的距离为 ,求新建管道的总长度.(结果精确到 , , , , )
22. 共抓长江大保护,建设水墨丹青新岳阳,推进市中心城区污水系统综合治理项目,需要从如图A,B两地向 地新建 , 两条笔直的污水收集管道,现测得C地在A地北偏东 方向上,在B地北偏西 方向上, 的距离为 ,求新建管道的总长度.(结果精确到 , , , , ) 23. 如图1,在矩形 中, ,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边 上沿 , 的方向运动,当点Q运动到点 时, 两点同时停止运动,设点P运动的时间为 ,连接 ,过点P作 , 与边 相交于点E,连接 .
23. 如图1,在矩形 中, ,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边 上沿 , 的方向运动,当点Q运动到点 时, 两点同时停止运动,设点P运动的时间为 ,连接 ,过点P作 , 与边 相交于点E,连接 .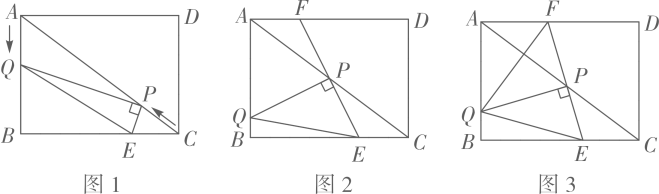 (1)、如图2,当 时,延长 交边 于点F.求证: ;(2)、在(1)的条件下,试探究线段 三者之间的等量关系,并加以证明;(3)、如图3,当 时,延长 交边 于点 ,连接 ,若 平分 ,求 的值.24. 如图1所示,在平面直角坐标系中,抛物线 与 轴交于点 和点B,与y轴交于点C.
(1)、如图2,当 时,延长 交边 于点F.求证: ;(2)、在(1)的条件下,试探究线段 三者之间的等量关系,并加以证明;(3)、如图3,当 时,延长 交边 于点 ,连接 ,若 平分 ,求 的值.24. 如图1所示,在平面直角坐标系中,抛物线 与 轴交于点 和点B,与y轴交于点C.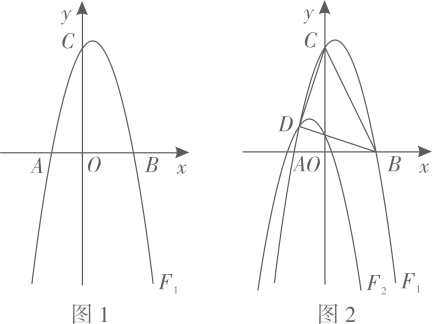 (1)、求抛物线 的表达式;(2)、如图2,将抛物线 先向左平移1个单位,再向下平移3个单位,得到抛物线 ,若抛物线 与抛物线 相交于点D,连接 , , .
(1)、求抛物线 的表达式;(2)、如图2,将抛物线 先向左平移1个单位,再向下平移3个单位,得到抛物线 ,若抛物线 与抛物线 相交于点D,连接 , , .①求点D的坐标;
②判断 的形状,并说明理由;
(3)、在(2)的条件下,抛物线 上是否存在点P,使得 为等腰直角三角形,若存在,求出点P的坐标;若不存在,请说明理由.