湖南省湘西市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
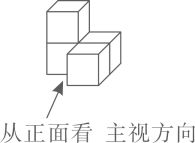
1. 下列各数中,比 小的数是( )A、0 B、-1 C、-3 D、32. 2019年中国与“一带一路”沿线国家货物贸易进出口总额达到92700亿元.用科学记数法表示92700是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由4个相同的小正方体组成的一个水平放置的立体图形,其箭头所指方向为主视方向,其俯视图是( )
 A、
A、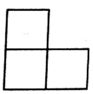 B、
B、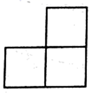 C、
C、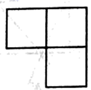 D、
D、 5. 从长度分别为 、 、 、 四条线段中随机取出三条,则能够组成三角形的概率为( )A、 B、 C、 D、6. 已知 ,作 的平分线 ,在射线 上截取线段 ,分别以O、C为圆心,大于 的长为半径画弧,两弧相交于E,F.画直线 ,分别交 于D,交 于G.那么, 一定是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形7. 已知正比例函数 的图象与反比例函数 的图象相交于点 ,下列说法正确的是( )A、正比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、正比例函数 与反比例函数 都随x的增大而增大 D、当 或 时,8. 如图, 、 为⊙O的切线,切点分别为A、B, 交 于点C, 的延长线交⊙O于点D.下列结论不一定成立的是( )
5. 从长度分别为 、 、 、 四条线段中随机取出三条,则能够组成三角形的概率为( )A、 B、 C、 D、6. 已知 ,作 的平分线 ,在射线 上截取线段 ,分别以O、C为圆心,大于 的长为半径画弧,两弧相交于E,F.画直线 ,分别交 于D,交 于G.那么, 一定是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形7. 已知正比例函数 的图象与反比例函数 的图象相交于点 ,下列说法正确的是( )A、正比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、正比例函数 与反比例函数 都随x的增大而增大 D、当 或 时,8. 如图, 、 为⊙O的切线,切点分别为A、B, 交 于点C, 的延长线交⊙O于点D.下列结论不一定成立的是( )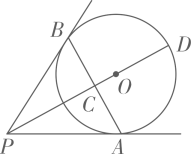 A、 为等腰三角形 B、 与 相互垂直平分 C、点C、B都在以 为直径的圆上 D、 为 的边 上的中线9. 如图,在平面直角坐标系 中,矩形 的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边 .则点C到x轴的距离等于( )
A、 为等腰三角形 B、 与 相互垂直平分 C、点C、B都在以 为直径的圆上 D、 为 的边 上的中线9. 如图,在平面直角坐标系 中,矩形 的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边 .则点C到x轴的距离等于( ) A、 B、 C、 D、10. 已知二次函数 图象的对称轴为 ,其图象如图所示,现有下列结论:① ;② ;③ ;④ ;⑤ .正确的是( )
A、 B、 C、 D、10. 已知二次函数 图象的对称轴为 ,其图象如图所示,现有下列结论:① ;② ;③ ;④ ;⑤ .正确的是( )
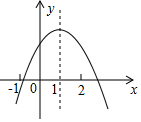 A、①③ B、②⑤ C、③④ D、④⑤
A、①③ B、②⑤ C、③④ D、④⑤二、填空题
-
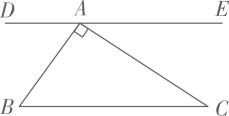
11. - 的绝对值是。12. 分解因式: = .13. 若多边形的内角和是外角和的2倍,则该多边形是边形.14. 不等式组 的解集为 .15. 如图,直线 ∥ , ,若 ,则 度.
 16. 从甲、乙两种玉米种子中选择一种合适的推荐给某地.考虑到庄稼人对玉米的产量和产量的稳定性十分的关心,选择之前,为了解甲、乙两种玉米种子的情况,某单位各用了10块自然条件相同的试验田进行试验,得到各试验田每公顷产量(单位:t)的数据,这两组数据的平均数分别是 甲 , 乙 ,方差分别是 2甲 2乙 ,你认为应该选择的玉米种子是 .17. 在平面直角坐标系中,O为原点,点 ,点B在y轴的正半轴上, .矩形 的顶点D,E,C分别在 上, .将矩形 沿x轴向右平移,当矩形 与 重叠部分的面积为 时,则矩形 向右平移的距离为 .
16. 从甲、乙两种玉米种子中选择一种合适的推荐给某地.考虑到庄稼人对玉米的产量和产量的稳定性十分的关心,选择之前,为了解甲、乙两种玉米种子的情况,某单位各用了10块自然条件相同的试验田进行试验,得到各试验田每公顷产量(单位:t)的数据,这两组数据的平均数分别是 甲 , 乙 ,方差分别是 2甲 2乙 ,你认为应该选择的玉米种子是 .17. 在平面直角坐标系中,O为原点,点 ,点B在y轴的正半轴上, .矩形 的顶点D,E,C分别在 上, .将矩形 沿x轴向右平移,当矩形 与 重叠部分的面积为 时,则矩形 向右平移的距离为 .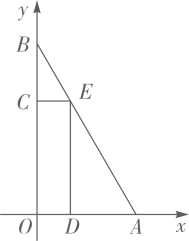 18. 观察下列结论:
18. 观察下列结论:⑴如图①,在正三角形 中,点M,N是 上的点,且 ,则 , ;
⑵如图②,在正方形 中,点M,N是 上的点,且 ,则 , ;
⑶如图③,在正五边形 中,点M,N是 上的点,且 ,则 , ;……
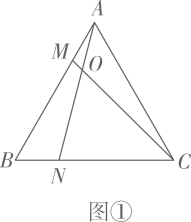
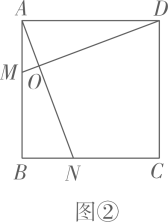
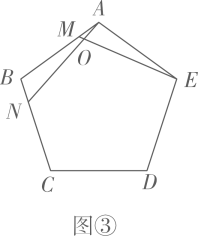
根据以上规律,在正n边形 中,对相邻的三边实施同样的操作过程,即点M,N是 上的点,且 , 与 相交于O.也会有类似的结论.你的结论是 .
三、解答题
-
19. 计算: .20. 化简: .21. 如图,在正方形 的外侧,作等边角形 ,连接 、 .
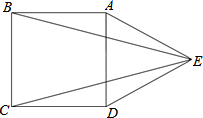 (1)、求证: ;(2)、求 的度数.22. 为加强安全教育,某校开展了“防溺水”安全知识竞赛,想了解七年级学生对“防溺水”安全知识的掌握情况.现从七年级学生中随机抽取50名学生进行竞赛,并将他们的竞赛成绩(百分制)进行整理、描述和分析.部分信息如下:
(1)、求证: ;(2)、求 的度数.22. 为加强安全教育,某校开展了“防溺水”安全知识竞赛,想了解七年级学生对“防溺水”安全知识的掌握情况.现从七年级学生中随机抽取50名学生进行竞赛,并将他们的竞赛成绩(百分制)进行整理、描述和分析.部分信息如下:a.七年级参赛学生成绩频数分布直方图(数据分成五组: , , , , )如图所示
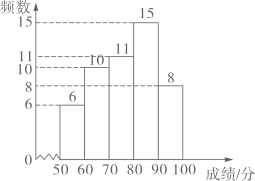
b.七年级参赛学生成绩在 这一组的具体得分是:70,71,73,75,76,76,76,77,77,78 ,79
c.七年级参赛学生成绩的平均数、中位数、众数如下:
年级
平均数
中位数
众数
七
76.9
m
80
d.七年级参赛学生甲的竞赛成绩得分为79分.
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在75分以上(含75分)的有人;(2)、表中m的值为;(3)、在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第名;(4)、该校七年级学生有500人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.23. 某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?24. 如图, 是⊙O的直径, 是⊙O的切线, 交⊙O于点E.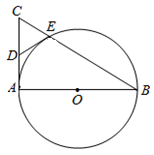 (1)、若D为 的中点,证明: 是⊙O的切线;(2)、若 , ,求⊙O的半径 的长.25. 如图
(1)、若D为 的中点,证明: 是⊙O的切线;(2)、若 , ,求⊙O的半径 的长.25. 如图  (1)、问题背景:如图1,在四边形 中, , , , , , 绕B点旋转,它的两边分别交 、 于E、F.探究图中线段 , , 之间的数量关系.小李同学探究此问题的方法是:延长 到G,使 ,连接 ,先证明 ,再证明 ,可得出结论,他的结论就是;(2)、探究延伸1:如图2,在四边形 中, , , , , 绕B点旋转,它的两边分别交 、 于E、F.上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由.(3)、探究延伸2:如图3,在四边形 中, , , , 绕B点旋转,它的两边分别交 、 于E、F.上述结论是否仍然成立?并说明理由.(4)、实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西 的A处舰艇乙在指挥中心南偏东 的B处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东 的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且指挥中心观测两舰艇视线之间的夹角为 ,试求此时两舰艇之间的距离.26. 已知直线 与抛物线 (b,c为常数, )的一个交点为 ,点 是x轴正半轴上的动点.(1)、当直线 与抛物线 (b,c为常数, )的另一个交点为该抛物线的顶点E时,求k,b,c的值及抛物线顶点E的坐标;(2)、在(1)的条件下,设该抛物线与y轴的交点为C,若点Q在抛物线上,且点Q的横坐标为b,当 时,求m的值;(3)、点D在抛物线上,且点D的横坐标为 ,当 的最小值多 时,求b的值.
(1)、问题背景:如图1,在四边形 中, , , , , , 绕B点旋转,它的两边分别交 、 于E、F.探究图中线段 , , 之间的数量关系.小李同学探究此问题的方法是:延长 到G,使 ,连接 ,先证明 ,再证明 ,可得出结论,他的结论就是;(2)、探究延伸1:如图2,在四边形 中, , , , , 绕B点旋转,它的两边分别交 、 于E、F.上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由.(3)、探究延伸2:如图3,在四边形 中, , , , 绕B点旋转,它的两边分别交 、 于E、F.上述结论是否仍然成立?并说明理由.(4)、实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西 的A处舰艇乙在指挥中心南偏东 的B处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东 的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且指挥中心观测两舰艇视线之间的夹角为 ,试求此时两舰艇之间的距离.26. 已知直线 与抛物线 (b,c为常数, )的一个交点为 ,点 是x轴正半轴上的动点.(1)、当直线 与抛物线 (b,c为常数, )的另一个交点为该抛物线的顶点E时,求k,b,c的值及抛物线顶点E的坐标;(2)、在(1)的条件下,设该抛物线与y轴的交点为C,若点Q在抛物线上,且点Q的横坐标为b,当 时,求m的值;(3)、点D在抛物线上,且点D的横坐标为 ,当 的最小值多 时,求b的值.