湖南省衡阳市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. -3相反数是( )A、3 B、-3 C、 D、2. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 2019年12月12日,国务院新闻办公室发布,南水北调工程全面通水5周年来,直接受益人口超过1.2亿人,其中1.2亿用科学记数法表示为( )A、 B、 C、 D、4. 下列各式中正确的是( )A、 B、 C、 D、5. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、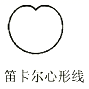 C、
C、 D、
D、 6. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、7. 如图,在四边形ABCD中,AC与BD相交于点O , 下列条件不能判定四边形ABCD为平行四边形的是( )
6. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、7. 如图,在四边形ABCD中,AC与BD相交于点O , 下列条件不能判定四边形ABCD为平行四边形的是( )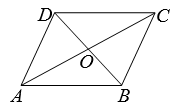 A、AB∥DC , AB=DC B、AB=DC , AD=BC C、AB∥DC , AD=BC D、OA=OC , OB=OD8. 下列不是三棱柱展开图的是( )A、
A、AB∥DC , AB=DC B、AB=DC , AD=BC C、AB∥DC , AD=BC D、OA=OC , OB=OD8. 下列不是三棱柱展开图的是( )A、 B、
B、 C、
C、 D、
D、 9. 不等式组 的解集在数轴上表示正确的是( )A、
9. 不等式组 的解集在数轴上表示正确的是( )A、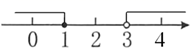 B、
B、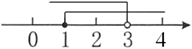 C、
C、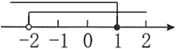 D、
D、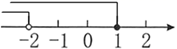 10. 反比例函数 经过点 ,则下列说法错误的是( )A、 B、函数图象分布在第一、三象限 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小11. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( )
10. 反比例函数 经过点 ,则下列说法错误的是( )A、 B、函数图象分布在第一、三象限 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小11. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( ) A、 B、 C、 D、12. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )
A、 B、 C、 D、12. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )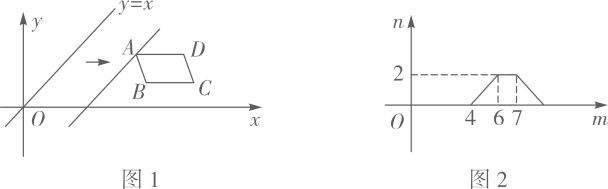 A、3 B、 C、6 D、
A、3 B、 C、6 D、二、填空题
-
13. 因式分解: .14. 计算: .15. 已知一个n边形的每一个外角都为30°,则n等于 .16. 一副三角板如图摆放,且 ,则∠1的度数为 .
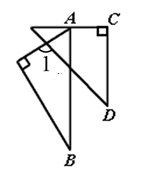 17. 某班有52名学生,其中男生人数是女生人数的2倍少17人,则女生有名.18. 如图,在平面直角坐标系中,点 的坐标 ,将线段 绕点O按顺时针方向旋转45°,再将其长度伸长为 的2倍,得到线段 ;又将线段 绕点O按顺时针方向旋转45°,长度伸长为 的2倍,得到线段 ;如此下去,得到线段 、 ,……, (n为正整数),则点 的坐标是 .
17. 某班有52名学生,其中男生人数是女生人数的2倍少17人,则女生有名.18. 如图,在平面直角坐标系中,点 的坐标 ,将线段 绕点O按顺时针方向旋转45°,再将其长度伸长为 的2倍,得到线段 ;又将线段 绕点O按顺时针方向旋转45°,长度伸长为 的2倍,得到线段 ;如此下去,得到线段 、 ,……, (n为正整数),则点 的坐标是 .
三、解答题
-
19. 化简: .20. 一个不透明的盒子里装有除颜色外其余均相同的2个黑球和n个白球,搅匀后从盒子里随机摸出一个球,摸到白球的概率为 .(1)、求n的值;(2)、所有球放入盒中,搅匀后随机从中摸出1个球,放回搅匀,再随机摸出第2个球,求两次摸球摸到一个白球和一个黑球的概率,请用画树状图或列表的方法进行说明.21. 如图,在 中, ,过 的中点D作 , ,垂足分别为点E、F.
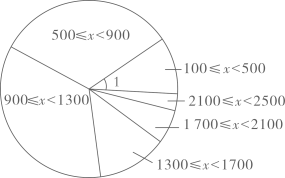
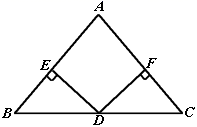 (1)、求证: ;(2)、若 ,求 的度数.22. 病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组: , , , , , .)
(1)、求证: ;(2)、若 ,求 的度数.22. 病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组: , , , , , .)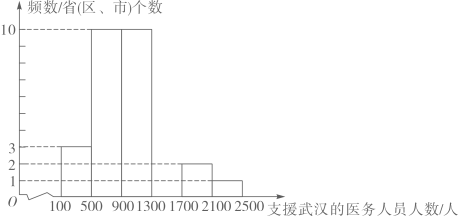
根据以上信息回答问题:
(1)、补全频数分布直方图.(2)、求扇形统计图中派出人数大于等于100小于500所占圆心角度数.据新华网报道在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
市派出的1614名医护人员中有404人是“90后”;
市派出的338名医护人员中有103人是“90后”;
市某医院派出的148名医护人员中有83人是“90后”.
(3)、请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)23. 小华同学将笔记本电脑水平放置在桌子上,当是示屏的边缘线 与底板的边缘线 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上, , , .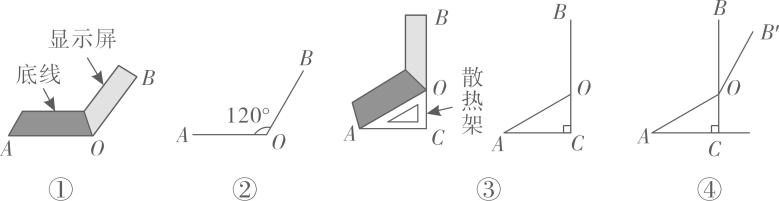 (1)、求 的长;(2)、如图④,垫入散热架后,要使显示屏的边缘线 与水平线的夹角仍保持120°,求点 到 的距离.(结果保留根号)24. 如图,在 中, , 平分 交 于点D,过点A和点D的圆,圆心O在线段 上, 交 于点E,交 于点F.
(1)、求 的长;(2)、如图④,垫入散热架后,要使显示屏的边缘线 与水平线的夹角仍保持120°,求点 到 的距离.(结果保留根号)24. 如图,在 中, , 平分 交 于点D,过点A和点D的圆,圆心O在线段 上, 交 于点E,交 于点F. (1)、判断 与 的位置关系,并说明理由;(2)、若 , ,求 的长.25. 在平面直角坐标系 中,关于x的二次函数 的图象过点 , .
(1)、判断 与 的位置关系,并说明理由;(2)、若 , ,求 的长.25. 在平面直角坐标系 中,关于x的二次函数 的图象过点 , . (1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.26. 如图1,平面直角坐标系 中,等腰 的底边 在x轴上, ,顶点A在y的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点F从点C出发,以相同的速度沿 向左运动,到达点O停止.已知点E、F同时出发,以 为边作正方形 ,使正方形 和 在 的同侧.设运动的时间为 秒( ).
(1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.26. 如图1,平面直角坐标系 中,等腰 的底边 在x轴上, ,顶点A在y的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点F从点C出发,以相同的速度沿 向左运动,到达点O停止.已知点E、F同时出发,以 为边作正方形 ,使正方形 和 在 的同侧.设运动的时间为 秒( ).
 (1)、当点H落在 边上时,求t的值;(2)、设正方形 与 重叠面积为S,请问是存在t值,使得 ?若存在,求出t值;若不存在,请说明理由;(3)、如图2,取 的中点D,连结 ,当点E、F开始运动时,点N从点O出发,以每秒 个单位的速度沿 运动,到达点O停止运动.请问在点E的整个运动过程中,点M可能在正方形 内(含边界)吗?如果可能,求出点M在正方形 内(含边界)的时长;若不可能,请说明理由.
(1)、当点H落在 边上时,求t的值;(2)、设正方形 与 重叠面积为S,请问是存在t值,使得 ?若存在,求出t值;若不存在,请说明理由;(3)、如图2,取 的中点D,连结 ,当点E、F开始运动时,点N从点O出发,以每秒 个单位的速度沿 运动,到达点O停止运动.请问在点E的整个运动过程中,点M可能在正方形 内(含边界)吗?如果可能,求出点M在正方形 内(含边界)的时长;若不可能,请说明理由.