湖南省常德市2020年中考数学试卷

试卷更新日期：2020-07-28 类型：中考真卷

进入出卷网下载

一、单选题

1. 4的倒数为（）

A、 $\frac{1}{4}$ B、2 C、1 D、﹣4

查看试题解析
2. 下面几种中式窗户图形既是轴对称又是中心对称的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，已知AB∥DE ， ∠1＝30°，∠2＝35°，则∠BCE的度数为（）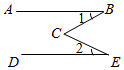

A、70° B、65° C、35° D、5°

查看试题解析
4. 下列计算正确的是（）

A、a²+b²＝（a+b）² B、a²+a⁴＝a⁶ C、a¹⁰÷a⁵＝a² D、a²•a³＝a⁵

查看试题解析
5. 下列说法正确的是（）

A、明天的降水概率为80%，则明天80%的时间下雨，20%的时间不下雨 B、抛掷一枚质地均匀的硬币两次，必有一次正面朝上 C、了解一批花炮的燃放质量，应采用抽样调查方式 D、一组数据的众数一定只有一个

查看试题解析
6. 一个圆锥的底面半径r＝10，高h＝20，则这个圆锥的侧面积是（）

A、100 $\sqrt{3}$ π B、200 $\sqrt{3}$ π C、100 $\sqrt{5}$ π D、200 $\sqrt{5}$ π

查看试题解析
7. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，下列结论：①b²﹣4ac＞0；②abc＜0；③4a+b＝0；④4a﹣2b+c＞0．其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
8. 如图，将一枚跳棋放在七边形ABCDEFG的顶点A处，按顺时针方向移动这枚跳棋2020次．移动规则是：第k次移动k个顶点（如第一次移动1个顶点，跳棋停留在B处，第二次移动2个顶点，跳棋停留在D处），按这样的规则，在这2020次移动中，跳棋不可能停留的顶点是（）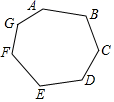

A、C、E B、E、F C、G、C、E D、E、C、F

查看试题解析

二、填空题

9. 分解因式： $x y^{2} - 4 x =$ ．

查看试题解析
10. 若代数式 $\frac{2}{\sqrt{2 x - 6}}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
11. 计算： $\sqrt{\frac{9}{2}}$ ﹣ $\sqrt{\frac{1}{2}} + \sqrt{8}$ ＝．

查看试题解析
12. 如图，若反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象经过点A ， AB⊥x轴于B ，且△AOB的面积为6，则k＝．

查看试题解析
13. 4月23日是世界读书日，这天某校为了解学生课外阅读情况，随机收集了30名学生每周课外阅读的时间，统计如表：

阅读时间（x小时）

x≤3.5

3.5＜x≤5

5＜x≤6.5

x＞6.5

人数

12

8

6

4

若该校共有1200名学生，试估计全校每周课外阅读时间在5小时以上的学生人数为．

查看试题解析
14. 今年新冠病毒疫情初期，口罩供应短缺，某地规定：每人每次限购5只．李红出门买口罩时，无论是否买到，都会消耗家里库存的口罩一只，如果有口罩买，他将买回5只．已知李红家原有库存15只，出门10次购买后，家里现有口罩35只．请问李红出门没有买到口罩的次数是次．

查看试题解析
15. 如图1，已知四边形ABCD是正方形，将 $△ D A E$ ， $△ D C F$ 分别沿DE ， DF向内折叠得到图2，此时DA与DC重合（A、C都落在G点），若GF＝4，EG＝6，则DG的长为．

查看试题解析
16. 阅读理解：对于x³﹣（n²+1）x+n这类特殊的代数式可以按下面的方法分解因式：
x³﹣（n²+1）x+n＝x³﹣n²x﹣x+n＝x（x²﹣n²）﹣（x﹣n）＝x（x﹣n）（x+n）﹣（x﹣n）＝（x﹣n）（x²+nx﹣1）．

理解运用：如果x³﹣（n²+1）x+n＝0，那么（x﹣n）（x²+nx﹣1）＝0，即有x﹣n＝0或x²+nx﹣1＝0，

因此，方程x﹣n＝0和x²+nx﹣1＝0的所有解就是方程x³﹣（n²+1）x+n＝0的解．

解决问题：求方程x³﹣5x+2＝0的解为．

查看试题解析

三、解答题

17. 计算：2⁰+（ $\frac{1}{3}$ ）^﹣¹• $\sqrt{4}$ ﹣4tan45°．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 x - 1 < x + 4 ① \\ \frac{2}{3} x - \frac{3 x + 1}{2} \leq \frac{1}{3} ② \end{array}$ ．

查看试题解析
19. 先化简，再选一个合适的数代入求值：（x+1﹣ $\frac{7 x - 9}{x}$ ）÷ $\frac{x^{2} - 9}{x}$ ．

查看试题解析
20. 第5代移动通信技术简称5G ，某地已开通5G业务，经测试5G下载速度是4G下载速度的15倍，小明和小强分别用5G与4G下载一部600兆的公益片，小明比小强所用的时间快140秒，求该地4G与5G的下载速度分别是每秒多少兆？

查看试题解析
21. 已知一次函数y＝kx+b（k≠0）的图象经过A（3，18）和B（﹣2，8）两点．

(1)、求一次函数的解析式；

(2)、若一次函数y＝kx+b（k≠0）的图象与反比例函数y＝ $\frac{m}{x}$ （m≠0）的图象只有一个交点，求交点坐标．

查看试题解析
22. 如图1是自动卸货汽车卸货时的状态图，图2是其示意图．汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方，AB与水平线AD之间的夹角是5°，卸货时，车厢与水平线AD成60°，此时AB与支撑顶杆BC的夹角为45°，若AC＝2米，求BC的长度．（结果保留一位小数）

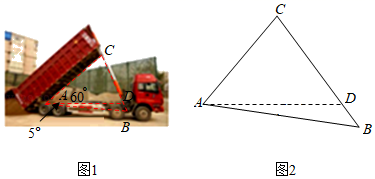
（参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75， $\sqrt{2}$ ≈1.41）

查看试题解析
23. 今年2﹣4月某市出现了200名新冠肺炎患者，市委根据党中央的决定，对患者进行了免费治疗．图1是该市轻症、重症、危重症三类患者的人数分布统计图（不完整），图2是这三类患者的人均治疗费用统计图．请回答下列问题．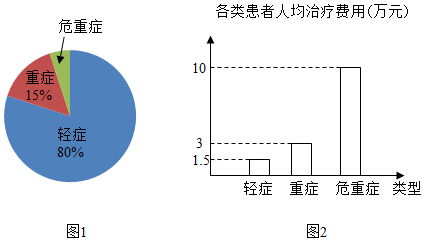

(1)、轻症患者的人数是多少？

(2)、该市为治疗危重症患者共花费多少万元？

(3)、所有患者的平均治疗费用是多少万元？

(4)、由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的A、B、C、D、E五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中B、D两位患者的概率．

查看试题解析
24. 如图，已知AB是⊙O的直径，C是⊙O上的一点，D是AB上的一点，DE⊥AB于D ， DE交BC于F ，且EF＝EC ．

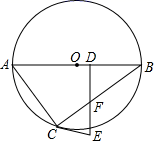(1)、求证：EC是⊙O的切线；

(2)、若BD＝4，BC＝8，圆的半径OB＝5，求切线EC的长．

查看试题解析
25. 如图，已知抛物线y＝ax²过点A（﹣3， $\frac{9}{4}$ ）．

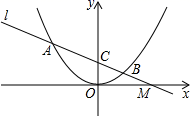(1)、求抛物线的解析式；

(2)、已知直线l过点A ， M（ $\frac{3}{2}$ ，0）且与抛物线交于另一点B ，与y轴交于点C ，求证：MC²＝MA•MB；

(3)、若点P ， D分别是抛物线与直线l上的动点，以OC为一边且顶点为O ， C ， P ， D的四边形是平行四边形，求所有符合条件的P点坐标．

查看试题解析
26. 已知D是Rt△ABC斜边AB的中点，∠ACB＝90°，∠ABC＝30°，过点D作Rt△DEF使∠DEF＝90°，∠DFE＝30°，连接CE并延长CE到P ，使EP＝CE ，连接BE ， FP ， BP ，设BC与DE交于M ， PB与EF交于N ．

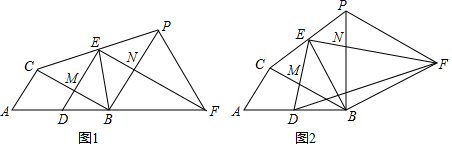(1)、如图1，当D ， B ， F共线时，求证：
①EB＝EP；

②∠EFP＝30°；

(2)、如图2，当D ， B ， F不共线时，连接BF ，求证：∠BFD+∠EFP＝30°．

查看试题解析

阅读时间（x小时）	x≤3.5	3.5＜x≤5	5＜x≤6.5	x＞6.5
人数	12	8	6	4