浙江省杭州市萧山区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-28 类型:期末考试
一、选择题:本题有10小题,每小题3分,共30分。
-
1. 下列四个几何图形中是中心对称图形的是( )A、
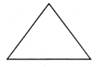 B、
B、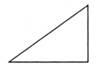 C、
C、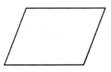 D、
D、 2. 二次根式 中字母x的取值可以是( )A、 B、0 C、 D、-13. 已知y是关于x的反比例函数,且当x= 时,y=2。则y关于x的函数表达式为( )A、y=-x B、y= C、y= x D、y=4. 如表记录了甲、乙、丙、丁四名学生近5次数学成绩的数据信息,要选择一名成绩好又发挥稳定的学生参加年级数学比赛,应该选择的是( )
2. 二次根式 中字母x的取值可以是( )A、 B、0 C、 D、-13. 已知y是关于x的反比例函数,且当x= 时,y=2。则y关于x的函数表达式为( )A、y=-x B、y= C、y= x D、y=4. 如表记录了甲、乙、丙、丁四名学生近5次数学成绩的数据信息,要选择一名成绩好又发挥稳定的学生参加年级数学比赛,应该选择的是( )甲
乙
丙
丁
平均数 (分)
110
103
110
107
方差S2(分²)
2.5
2.5
10.3
6.5
A、甲 B、乙 C、丙 D、丁5. 化简 ,正确的是( )A、2 B、 C、6 D、6. 下列用配方法解方程 x2-x-2=0的四个步骤中,出现错误的是( ) A、① B、② C、③ D、④7. 如图,在 ABCD中,E是CD上一点,BE=BC。若∠A:∠ADC=1:2,则∠ABE的度数是( )
A、① B、② C、③ D、④7. 如图,在 ABCD中,E是CD上一点,BE=BC。若∠A:∠ADC=1:2,则∠ABE的度数是( )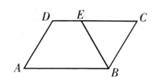 A、70° B、65° C、60° D、55°8. 如图,一块长方形绿地的长为100m,宽为50m,在绿地中开辟两条道路后剩余绿地面积为4704m²。则根据题意可列出方程( )
A、70° B、65° C、60° D、55°8. 如图,一块长方形绿地的长为100m,宽为50m,在绿地中开辟两条道路后剩余绿地面积为4704m²。则根据题意可列出方程( )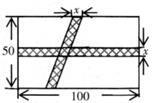 A、5000-150x=4704 B、5000-150x+x2=4704 C、5000-150x-x2=4704 D、5000-150x+ x2=47049. 已知反比例函数y= ,给出下列结论:①该函数图象在一、三象限;②若x>3,则0<y<1;③若点(m-n, ),(m-p, )在该函数图象上,则m>n>p。其中正确的是( )A、①② B、②③ C、①③ D、①②③10. 如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为8 ,最小值为8,则菱形ABCD的边长为( )
A、5000-150x=4704 B、5000-150x+x2=4704 C、5000-150x-x2=4704 D、5000-150x+ x2=47049. 已知反比例函数y= ,给出下列结论:①该函数图象在一、三象限;②若x>3,则0<y<1;③若点(m-n, ),(m-p, )在该函数图象上,则m>n>p。其中正确的是( )A、①② B、②③ C、①③ D、①②③10. 如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为8 ,最小值为8,则菱形ABCD的边长为( ) A、4 B、10 C、12 D、16
A、4 B、10 C、12 D、16二、填空题:本题有6个小题,每小题4分,共24分
-
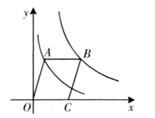
11. 计算:( )²= 。12. 已知一个多边形的内角和等于外角和的3倍,则这个多边形的边数为 。13. 已知一组数据1,3,5,x,y的平均数是3,则另一组数据-1,1,3,x-2,y-2的平均数是。14. 把关于y的方程(2y-3)2=y(y-2)化成一般形式为。15. 如图,已知 OABC的顶点A,B分别在反比例函数y= (x>0)和y= (x>0)的图象上。若 OABC的面积为6,则k=。
 16. 如图,正方形ABCD的边长为4,E为边AD上一动点,连结BE,CE,以CE为边向右侧作正方形CEFG。
16. 如图,正方形ABCD的边长为4,E为边AD上一动点,连结BE,CE,以CE为边向右侧作正方形CEFG。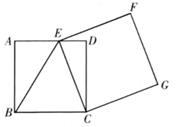 (1)、若BE=5,则正方形CEFG的面积为。(2)、连结DF,DG,则△DFG面积的最小值为。
(1)、若BE=5,则正方形CEFG的面积为。(2)、连结DF,DG,则△DFG面积的最小值为。三、解答题:本题有7小题,共66分.解答应写出文字说明,证明过程或推演步骤.
-
17. 计算:(1)、(2)、18. 在抗击“新冠肺炎疫情”的日子里,某校积极开展“停课不停学”的线上教学活动.为了解全校1200名学生一周内平均每天在家进行体育锻炼时间的情况,随机调查了该校100名学生一周内平均每天在家进行体育锻炼时间的情况,结果如下表:
时间(分)
15
20
25
30
35
40
45
50
55
56
人数
16
24
14
10
8
6
8
4
6
4
完成下列问题:
(1)、根据统计表信息,写出这100名学生一周内平均每天在家体育锻炼时间的中位数和众数。(2)、请估计该校一周内平均每天在家体育锻炼时间不少于35分钟的学生大约有多少人?19. 选用适当的方法解下列方程:(1)、(x-2)²=4(2)、2a2-5=3a20. 已知关于x的一元二次方程x2+4x=1-m。(1)、当m=5时,试判断此方程根的情况。(2)、若x1 , x2是该方程不相等的两实数根,且(x12+4x1)(x22+4x2)=49,求m的值。21. 已知:如图,在 ABCD中,延长DC至点E,使得DC=CE,连结AE交BC于点F。连结AC,BE。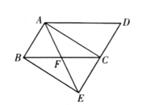 (1)、求证:四边形ABEC是平行四边形。(2)、若∠AFC=2∠D,求证:四边形ABEC是矩形。22. 已知反比例函数y= 。(1)、若点(-t+ ,-2)在此反比例函数图象上,求t的值。(2)、若点(x1 , y1)和(x2 , y2)是此反比例函数图象上的任意两点,
(1)、求证:四边形ABEC是平行四边形。(2)、若∠AFC=2∠D,求证:四边形ABEC是矩形。22. 已知反比例函数y= 。(1)、若点(-t+ ,-2)在此反比例函数图象上,求t的值。(2)、若点(x1 , y1)和(x2 , y2)是此反比例函数图象上的任意两点,①当x1>0,x2>0,且x1=x2+2时,求 的值;
②当x1>x2时,试比较y1 , y2的大小。
23. 如图①,已知正方形ABCD中,E,F分别是边AD,CD上的点(点E,F不与端点重合),且AE=DF,BE,AF交于点P,过点C作CH⊥BE交BE于点H。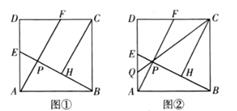 (1)、求证:AF∥CH。(2)、若AB=2 ,AE=2,试求线段PH的长。(3)、如图②,连结CP并延长交AD于点Q,若点H是BP的中点,试求 的值。
(1)、求证:AF∥CH。(2)、若AB=2 ,AE=2,试求线段PH的长。(3)、如图②,连结CP并延长交AD于点Q,若点H是BP的中点,试求 的值。