浙江省杭州市钱塘新区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-28 类型：期末考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分.

1. 下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 使二次根式 $\sqrt{m - 3}$ 有意义的m的取值范围是（）

A、m≥3 B、m>3 C、m≤3 D、m<3

查看试题解析
3. 关于反比例函数y= $- \frac{2}{x}$ ，下列说法正确的是（）

A、图象经过(1，2)点 B、图象在一、三象限 C、当x>0时，y随x的增大而减小 D、当x<0时，y随x的增大而增大

查看试题解析
4. 测试五位学生的“立定跳远”成绩，得到5个互不相同的数据，在统计时出现一处错误，将最低成绩写得更低了，计算不受影响的是（）

A、方差 B、标准差 C、平均数 D、中位数

查看试题解析
5. 用配方法解一元二次方程x²-8x+11=0，此方程可化为（）

A、(x-4)²=5 B、(x+4)²=5 C、(x-4)²=27 D、(x+4)²=27

查看试题解析
6. 若一个多边形的内角和是外角和的3倍，则这个多边形是（）

A、六边形 B、七边形 C、八边形 D、十边形

查看试题解析
7. 某小区中央花园有一块长方形花圃，它的宽为5m，若长边不变，将短边扩大，使得扩大后的花圃形状为正方形，且面积比原来增加15m²，设原来花圃长边为xm，可列方程（）

A、x²+5x=15 B、x²-5x=15 C、(x-5)²=15 D、x²-25=15

查看试题解析
8. 如图，在菱形ABCD中，E，F分别是BC，CD的中点，设S_{四边形ABCD}=S，S_△AEF=S₁ ，则（）

A、S₁= $\frac{1}{2}$ S B、S₁< $\frac{1}{2}$ S C、S₁> $\frac{1}{2}$ S D、5S₁=2S

查看试题解析
9. 如图，斜靠在墙上的一根竹竿，AB=5m，OB=3m。若B端沿地面OB方向外移0.5m，则A端沿垂直于地面AC方向下移（）

A、等于0.5m B、小于0.5m C、大于0.5m D、不确定

查看试题解析
10. 如图，在正方形ABCD中，点E是CD边上的一个动点(不与点C、D重合)，BE的垂直平分线分别交AD，BC于点F，G。若FD=5AF，则CE：ED的值为（）

A、6-2 $\sqrt{3}$ B、 $\frac{\sqrt{10} - 5}{2}$ C、 $\sqrt{3}$ -1 D、 $\frac{\sqrt{10}}{4}$

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分。

11. 当a=2时，二次根式 $\sqrt{a + 2}$ 的值是。

查看试题解析
12. 已知方程x²+mx+3=0的一个根是1，则m的值是。

查看试题解析
13. 已知3个正数a₁ ， a₂ ， a₃的平均数是a，则数据a₁ ， a₂ ， 0，a₃的平均数为。(用含a的代数式表示)

查看试题解析
14. 如图，在平行四边形ABCD中，AB=5，AD=7，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，则线段EF的长为。

查看试题解析
15. 如图，在平面直角坐标系中，菱形OABC的边OA在x轴的正半轴上，反比例函数y= $\frac{k}{x}$ (x>0)的图象经过对角线OB的中点D和顶点C。若菱形OABC的面积为6 $\sqrt{3}$ ，则k=。

查看试题解析
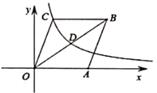16. 如图，正方形ABCD的边长为4，点E为CD边上的一个动点，以CE为边向外作正方形ECFG，连结BG，点H为BG中点，连结EH，则EH的最小值为。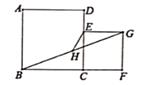

查看试题解析

三、解答题：本大题有7个小题，共66分.

17. 计算：

(1)、 $\sqrt{3} + \sqrt{6} \times \sqrt{8}$

(2)、 $\frac{\sqrt{2}}{\sqrt{2} - 1}$

查看试题解析
18. 解方程：

(1)、2(x-2)²=18.

(2)、2x(x+3)-x-3=0

查看试题解析
19. 如图，在平行四边形ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F，连结BF，DE。

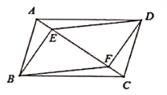(1)、求证：四边形BF DE是平行四边形；

(2)、连结BD，若BE=3，BF=5，求BD的长。

查看试题解析
20.

(1)、已知数据99，97，96，98，95，这组数据画成折线图(如图1)。将这组数据的每一个数都减去97，得到一组新数据，在图2中将这组数据画成折线图，则新数据的方差原数据的方差(填“大于”、“等于”、“小于”)。

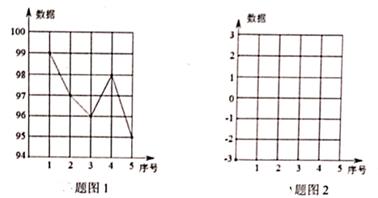(2)、已知数据5，3，2，4，1，这组数据画成折线图(如图3)。将这组数据的每一个数都乘以2，得到一组新数据，在图4中将这组数据画成折线图，则新数据的方差原数据的方差(填“大于”、“等于”、“小于”)。

(3)、已知甲组数据x₁ ， x₂ ， x₃的平均数为 $\bar{x 甲}$ ，方差为 $S_{甲}^{2}$ 。将这组数据的每一个数都乘以3再加上1，得到乙组数据x₁'=3x₁+1，x₂'=3x₂+1，x₃'=3x₃+1，它们的平均数为 $\bar{x 乙}$ ，方差为 $S_{乙}^{2}$ ，比较 $S_{甲}^{2}$ 与 $S_{乙}^{2}$ 的大小，并说明理由。

查看试题解析
21. 如图，在△ABC中、∠ACB=90°，以点B为圆心，BC长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E、连结CD。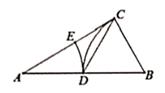

(1)、若∠A=26°，求∠ACD的度数。

(2)、设BC= $\frac{a}{2}$ ，AC=b，线段AE的长是方程x²+ax-b²=0的一个根吗？说明理由。

查看试题解析
22. 已知一次函数y=3x+m的图象与反比例函数y= $\frac{n}{x}$ 的图象交于点A(1，a)，B(-2，-3)。

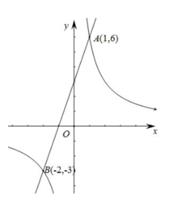(1)、求一次函数，反比例函数的表达式。

(2)、设点C(t，y₁)，D(t、y₂)分别是一次函数和反比例函数图象上的点，当y₁>y₂时，求t的取值范围。

(3)、设点E(x₁ ， 2)，F(x₂ ， 2)分别是一次函数和反比例函数图象上的点，点G是反比例函数图象上与点F成中心对称的点，求△GEF的面积。

查看试题解析
23. 图，在矩形ABCD中，点E是AD上的一点(不与点A，D重合)，△ABE沿BE折叠，得△BEF，点A的对称点为点F。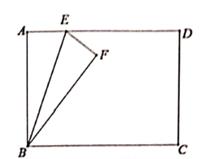

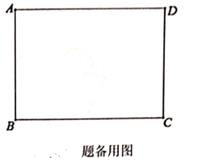(1)、当AB=AD时，点F会落在CE上吗？请说明理由。

(2)、设 $\frac{A B}{A D}$ =m(0<m<1)，且点F恰好落在CE上。
①求证：CF=DE。

②若 $\frac{A E}{A D}$ =n，用等式表示m，n的关系。

查看试题解析