黑龙江省牡丹江市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 函数y 中自变量x的取值范围是( )A、x>3 B、x≠3 C、x≥3 D、x≥04. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是( )
3. 函数y 中自变量x的取值范围是( )A、x>3 B、x≠3 C、x≥3 D、x≥04. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是( )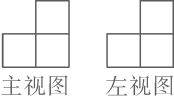 A、6 B、5 C、4 D、35. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、6. 如图,四边形 内接于 ,连接 .若 , ,则 的度数是( )
A、6 B、5 C、4 D、35. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、6. 如图,四边形 内接于 ,连接 .若 , ,则 的度数是( )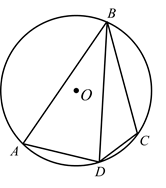 A、125° B、130° C、135° D、140°7. 一列数1,5,11,19…按此规律排列,第7个数是( )A、37 B、41 C、55 D、718. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.P为y轴上一点,连接 , .则 的面积为( )
A、125° B、130° C、135° D、140°7. 一列数1,5,11,19…按此规律排列,第7个数是( )A、37 B、41 C、55 D、718. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.P为y轴上一点,连接 , .则 的面积为( ) A、5 B、6 C、11 D、129. 若关于x的方程 的解为正数,则m的取值范围是( )A、 B、 且 C、 D、 且10. 如图,在平面直角坐标系中,O是菱形 对角线 的中点, 轴且 , ,将菱形 绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是( )
A、5 B、6 C、11 D、129. 若关于x的方程 的解为正数,则m的取值范围是( )A、 B、 且 C、 D、 且10. 如图,在平面直角坐标系中,O是菱形 对角线 的中点, 轴且 , ,将菱形 绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是( ) A、 B、 C、 D、 或11. 如图,在矩形 中, , ,点E在 边上, ,垂足为F.若 ,则线段 的长为( )
A、 B、 C、 D、 或11. 如图,在矩形 中, , ,点E在 边上, ,垂足为F.若 ,则线段 的长为( ) A、2 B、3 C、4 D、512. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )
A、2 B、3 C、4 D、512. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )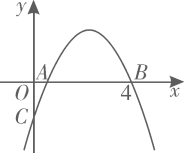 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
13. 新冠肺炎疫情期间,全国各地约42000名医护人员驰援湖北.请将数42000用科学记数法表示为 .14. 如图,在四边形 中,连接 , .请你添加一个条件 , 使 .(填一种情况即可)
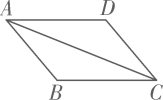 15. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .16. 某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使利润率为20%,则商店应打折.17. 是 的弦, ,垂足为M,连接 .若 中有一个角是30°, ,则弦 的长为 .18. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .19. 如图,在 中, ,点E在 边上.将 沿直线 翻折,点A落在点 处,连接 ,交 于点F.若 , ,则 .
15. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .16. 某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使利润率为20%,则商店应打折.17. 是 的弦, ,垂足为M,连接 .若 中有一个角是30°, ,则弦 的长为 .18. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .19. 如图,在 中, ,点E在 边上.将 沿直线 翻折,点A落在点 处,连接 ,交 于点F.若 , ,则 . 20. 如图,在 中, ,M是 的中点,点D在 上, , ,垂足分别为E,F,连接 .则下列结论中:① ;② ;③ ;④ ;⑤若 平分 ,则 ;⑥ ,正确的有 . (只填序号)
20. 如图,在 中, ,M是 的中点,点D在 上, , ,垂足分别为E,F,连接 .则下列结论中:① ;② ;③ ;④ ;⑤若 平分 ,则 ;⑥ ,正确的有 . (只填序号)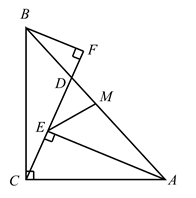
三、解答题
-
21. 先化简,再求值: ,其中 .22. 如图,抛物线 与x轴交于A,B两点,与y轴交于点C,抛物线的顶点为P.已知 .请解答下列问题:
 (1)、求抛物线的解析式,并直接写出点P的坐标;(2)、抛物线的对称轴与x轴交于点E,连接 , 的垂直平分线交直线 于点M,则线段 的长为 .
(1)、求抛物线的解析式,并直接写出点P的坐标;(2)、抛物线的对称轴与x轴交于点E,连接 , 的垂直平分线交直线 于点M,则线段 的长为 .注:抛物线 的对称轴是直线 ,顶点坐标是 .
23. 在 中, , , .以 为边作周长为18的矩形 ,M,N分别为 , 的中点,连接 .请你画出图形,并直接写出线段 的长.24. 某中学为了了解本校学生对排球、篮球、毽球、羽毛球和跳绳五项“大课间”活动的喜欢情况,随机抽查了部分学生进行问卷调查(每名学生只选择一项),将调查结果整理并绘制成如下不完整的统计图表.请结合统计图表解答下列问题:抽样调查学生喜欢大课间活动人数的统计表
项目
人数
A排球
6
B篮球
m
C毽球
10
D羽毛球
4
E跳绳
18
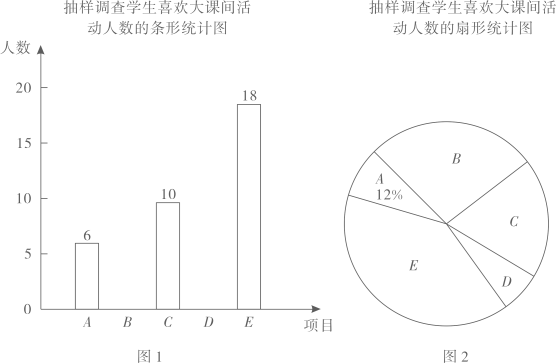 (1)、本次抽样调查的学生有人,请补全条形统计图;(2)、求扇形统计图中,喜欢毽球活动的学生人数所对应圆心角的度数;(3)、全校有学生1800人,估计全校喜欢跳绳活动的学生人数是多少?25. 在一条公路上依次有A,B,C三地,甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地停留0.5小时后,按原路原速返回C地,两车匀速行驶,甲车比乙车晚1.5小时到达C地.两车距各自出发地的路程y(千米)与时间x(小时)之间的函数关系如图所示.请结合图象信息解答下列问题:
(1)、本次抽样调查的学生有人,请补全条形统计图;(2)、求扇形统计图中,喜欢毽球活动的学生人数所对应圆心角的度数;(3)、全校有学生1800人,估计全校喜欢跳绳活动的学生人数是多少?25. 在一条公路上依次有A,B,C三地,甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地停留0.5小时后,按原路原速返回C地,两车匀速行驶,甲车比乙车晚1.5小时到达C地.两车距各自出发地的路程y(千米)与时间x(小时)之间的函数关系如图所示.请结合图象信息解答下列问题: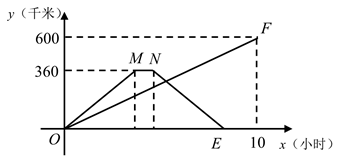 (1)、甲车行驶速度是千米1时,B,C两地的路程为千米;(2)、求乙车从B地返回C地的过程中,y(千米)与x(小时)之间的函数关系式(不需要写出自变量x的取值范围);(3)、出发多少小时,行驶中的两车之间的路程是15千米?请你直接写出答案.26. 在等腰 中, ,点D,E在射线 上, ,过点E作 ,交射线 于点F.请解答下列问题:
(1)、甲车行驶速度是千米1时,B,C两地的路程为千米;(2)、求乙车从B地返回C地的过程中,y(千米)与x(小时)之间的函数关系式(不需要写出自变量x的取值范围);(3)、出发多少小时,行驶中的两车之间的路程是15千米?请你直接写出答案.26. 在等腰 中, ,点D,E在射线 上, ,过点E作 ,交射线 于点F.请解答下列问题: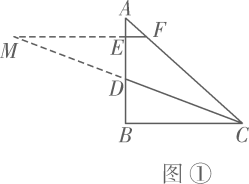
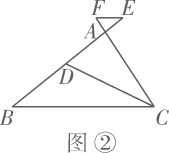
 (1)、当点E在线段 上, 是 的角平分线时,如图①,求证: ;(提示:延长 , 交于点M.)(2)、当点E在线段 的延长线上, 是 的角平分线时,如图②;当点E在线段 的延长线上, 是 的外角平分线时,如图③,请直接写出线段 , , 之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 ,则 .27. 某商场准备购进A,B两种书包,每个A种书包比B种书包的进价少20元,用700元购进A种书包的个数是用450元购进B种书包个数的2倍,A种书包每个标价是90元,B种书包每个标价是130元.请解答下列问题:(1)、A,B两种书包每个进价各是多少元?(2)、若该商场购进B种书包的个数比A种书包的2倍还多5个,且A种书包不少于18个,购进A,B两种书包的总费用不超过5450元,则该商场有哪几种进货方案?(3)、该商场按(2)中获利最大的方案购进书包,在销售前,拿出5个书包赠送给某希望小学,剩余的书包全部售出,其中两种书包共有4个样品,每种样品都打五折,商场仍获利1370元.请直接写出赠送的书包和样品中,A种,B种书包各有几个?28. 如图,已知直线 与x轴交于点A,与y轴交于点B,线段 的长是方程 的一个根, .请解答下列问题:
(1)、当点E在线段 上, 是 的角平分线时,如图①,求证: ;(提示:延长 , 交于点M.)(2)、当点E在线段 的延长线上, 是 的角平分线时,如图②;当点E在线段 的延长线上, 是 的外角平分线时,如图③,请直接写出线段 , , 之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 ,则 .27. 某商场准备购进A,B两种书包,每个A种书包比B种书包的进价少20元,用700元购进A种书包的个数是用450元购进B种书包个数的2倍,A种书包每个标价是90元,B种书包每个标价是130元.请解答下列问题:(1)、A,B两种书包每个进价各是多少元?(2)、若该商场购进B种书包的个数比A种书包的2倍还多5个,且A种书包不少于18个,购进A,B两种书包的总费用不超过5450元,则该商场有哪几种进货方案?(3)、该商场按(2)中获利最大的方案购进书包,在销售前,拿出5个书包赠送给某希望小学,剩余的书包全部售出,其中两种书包共有4个样品,每种样品都打五折,商场仍获利1370元.请直接写出赠送的书包和样品中,A种,B种书包各有几个?28. 如图,已知直线 与x轴交于点A,与y轴交于点B,线段 的长是方程 的一个根, .请解答下列问题: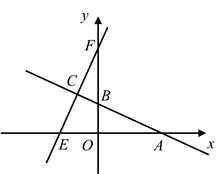 (1)、求点A,B的坐标;(2)、直线 交x轴负半轴于点E,交y轴正半轴于点F,交直线 于点C.若C是 的中点, ,反比例函数 图象的一支经过点C,求k的值;(3)、在(2)的条件下,过点C作 ,垂足为D,点M在直线 上,点N在直线 上.坐标平面内是否存在点P,使以D,M,N,P为顶点的四边形是正方形?若存在,请写出点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
(1)、求点A,B的坐标;(2)、直线 交x轴负半轴于点E,交y轴正半轴于点F,交直线 于点C.若C是 的中点, ,反比例函数 图象的一支经过点C,求k的值;(3)、在(2)的条件下,过点C作 ,垂足为D,点M在直线 上,点N在直线 上.坐标平面内是否存在点P,使以D,M,N,P为顶点的四边形是正方形?若存在,请写出点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.