黑龙江省哈尔滨市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. -8的倒数是( )A、 B、-8 C、8 D、2. 下列运算一定正确的是( )A、 B、 C、 D、3. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
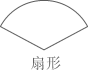 B、
B、 C、
C、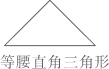 D、
D、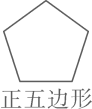 4. 五个大小相同的正方体塔成的几何体如图所示,其左视图是( )
4. 五个大小相同的正方体塔成的几何体如图所示,其左视图是( )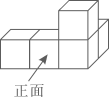 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图 是 直径,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( )
5. 如图 是 直径,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( )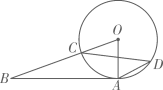 A、 B、 C、 D、6. 将抛物线 向上平移3个单位长度,再向右平移5个单位长度,所得的抛物线为( )A、 B、 C、 D、7. 如图,在 中, ,垂足为D, 与 关于直线AD对称,点的B对称点是 ,则 的度数是( )
A、 B、 C、 D、6. 将抛物线 向上平移3个单位长度,再向右平移5个单位长度,所得的抛物线为( )A、 B、 C、 D、7. 如图,在 中, ,垂足为D, 与 关于直线AD对称,点的B对称点是 ,则 的度数是( )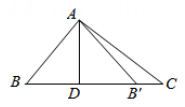 A、 B、 C、 D、8. 方程 的解是( )A、 B、 C、 D、9. 一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是( )A、 B、 C、 D、10. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )
A、 B、 C、 D、8. 方程 的解是( )A、 B、 C、 D、9. 一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是( )A、 B、 C、 D、10. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )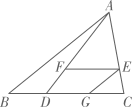 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将数4790000用科学记数法表示为 .12. 在函数 中,自变量x的取值范围是 .13. 已知反比例函数 的图像经过点 ,则k的值是 .14. 计算: 的结果是 .15. 把多项式 分解因式的结果是 .16. 抛物线 的顶点坐标为 .17. 不等式 的解集为 .18. 一个扇形的面积为 ,半径为6cm,则扇形的圆心角是度.19. 在 中, , 为BC边上的高, ,则BC的长为 .20. 如图,在菱形 中,对角线 相交于点O,点E在线段BO上,连接AE,若 , , ,则线段AE的长为 .
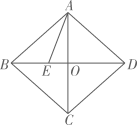
三、解答题
-
21. 先化简,再求代数式 的值,其中22. 如图,方格纸中每个小正方形的边长为1,线段AB和线段CD的端点均在小正方形的顶点上.
 (1)、在图中画出以AB为边的正方形 ,点E和点F均在小正方形的顶点上;(2)、在图中画出以CD为边的等腰三角形 ,点G在小正方形的顶点上,且 的周长为 ,连接EG,请直接写出线段EG的长.23. 为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢的哪一类?的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的 ,请你根据图中提供的信息回答下列问题:
(1)、在图中画出以AB为边的正方形 ,点E和点F均在小正方形的顶点上;(2)、在图中画出以CD为边的等腰三角形 ,点G在小正方形的顶点上,且 的周长为 ,连接EG,请直接写出线段EG的长.23. 为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢的哪一类?的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的 ,请你根据图中提供的信息回答下列问题: (1)、在这次调查中,一共抽取了多少名学生;(2)、请通过计算补全条形统计图;(3)、若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名.24. 已知,在 中, ,点D,点E在BC上, ,连接 .
(1)、在这次调查中,一共抽取了多少名学生;(2)、请通过计算补全条形统计图;(3)、若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名.24. 已知,在 中, ,点D,点E在BC上, ,连接 .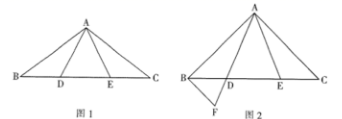 (1)、如图1,求证: ;(2)、如图2,当 时,过点B作 ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.25. 昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.(1)、求每个大地球仪和每个小地球仪各多少元;(2)、昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.26. 已知 是 的外接圆,AD为 的直径, ,垂足为E,连接BO,延长BO交AC于点F.
(1)、如图1,求证: ;(2)、如图2,当 时,过点B作 ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.25. 昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.(1)、求每个大地球仪和每个小地球仪各多少元;(2)、昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.26. 已知 是 的外接圆,AD为 的直径, ,垂足为E,连接BO,延长BO交AC于点F. (1)、如图1,求证: ;(2)、如图2,过点D作 ,交 于点G,点H为GD的中点,连接OH,求证: ;(3)、如图3,在(2)的条件下,连接CG,若 的面积为 ,求线段CG的长.27. 已知,在平面直角坐标系中,点O为坐标原点,直线 与x轴的正半轴交于点A,与y轴的负半轴交于点B, ,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为 ,过点C作 轴,垂足为 .
(1)、如图1,求证: ;(2)、如图2,过点D作 ,交 于点G,点H为GD的中点,连接OH,求证: ;(3)、如图3,在(2)的条件下,连接CG,若 的面积为 ,求线段CG的长.27. 已知,在平面直角坐标系中,点O为坐标原点,直线 与x轴的正半轴交于点A,与y轴的负半轴交于点B, ,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为 ,过点C作 轴,垂足为 .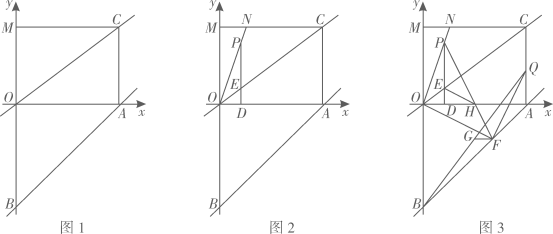 (1)、如图1,求直线 的解析式;(2)、如图2,点N在线段 上,连接ON,点P在线段ON上,过P点作 轴,垂足为D,交OC于点E,若 ,求 的值;(3)、如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,连接PF交x轴于点H,连接EH,若 ,求点P的坐标.
(1)、如图1,求直线 的解析式;(2)、如图2,点N在线段 上,连接ON,点P在线段ON上,过P点作 轴,垂足为D,交OC于点E,若 ,求 的值;(3)、如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,连接PF交x轴于点H,连接EH,若 ,求点P的坐标.